Seja f: R-->R definida por f(x)= ax-2.
Um
função é uma correspondência entre dois conjuntos. Se uma função f faz corresponder elementos de um conjunto A com os de um conjunto B então escrevemos f:A-->B.
Exemplo:
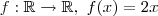
Note que estamos trabalhando com a "função dobro". Esta função pega cada numero real

e associa a seu dobro

. Ou seja, se

então

. Daí, escrevemos

. A função calculada para

vale

. Ok?
Poi bem. A sua função é

. Porém, o número

é incógnito neste caso. Temos de calculá-lo. Podemos fazer isso sabendo um ponto da função. O exercício diz que se você fizer x=-2 terá f= 10. Ou seja,

.
Daí, substituindo x=-2 e f=10 na expressão que define a função, temos


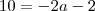

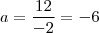
Daí,
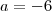
e , portanto,
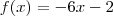
.
A
função inversa de f:A-->B é uma função g tal que

. Ou seja, a função inversa faz o "caminho inverso". Ela faz associar a cada elemento de B um de A. Entende? No exemplo da função dobro a função inversa é
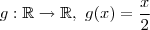
. É lógico: se f associa a cada x seu dobro então g deve associar a cada dobro o número que o concebeu, que é a metade do dobro(o original).
Mas, para um caso qualquer, calculamos a função inversa
trocando de lugar x e f(x) na expressão da f(x) e renomeando f como g, já que sabemos que g é a função inversa de f. Veja,
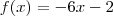
Torcando x e f(x) de lugar, temos

ou, corretamente,

.
Agora basta isolar a função g(x).

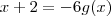
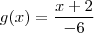
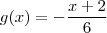
ou
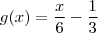
.
Entende?



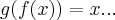 ...logo x=(f(x)+2)/a,como f(-2)=10=(-2)a-2
...logo x=(f(x)+2)/a,como f(-2)=10=(-2)a-2

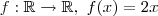
 e associa a seu dobro
e associa a seu dobro  . Ou seja, se
. Ou seja, se  então
então  . Daí, escrevemos
. Daí, escrevemos  . A função calculada para
. A função calculada para  . Ok?
. Ok? . Porém, o número
. Porém, o número  é incógnito neste caso. Temos de calculá-lo. Podemos fazer isso sabendo um ponto da função. O exercício diz que se você fizer x=-2 terá f= 10. Ou seja,
é incógnito neste caso. Temos de calculá-lo. Podemos fazer isso sabendo um ponto da função. O exercício diz que se você fizer x=-2 terá f= 10. Ou seja,  .
.

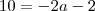

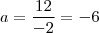
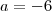 e , portanto,
e , portanto, 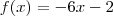 .
. . Ou seja, a função inversa faz o "caminho inverso". Ela faz associar a cada elemento de B um de A. Entende? No exemplo da função dobro a função inversa é
. Ou seja, a função inversa faz o "caminho inverso". Ela faz associar a cada elemento de B um de A. Entende? No exemplo da função dobro a função inversa é 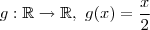 . É lógico: se f associa a cada x seu dobro então g deve associar a cada dobro o número que o concebeu, que é a metade do dobro(o original).
. É lógico: se f associa a cada x seu dobro então g deve associar a cada dobro o número que o concebeu, que é a metade do dobro(o original). ou, corretamente,
ou, corretamente,  .
.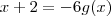
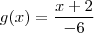
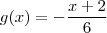
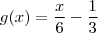 .
.