 por vspagnolo » Ter Nov 26, 2013 09:24
por vspagnolo » Ter Nov 26, 2013 09:24
Bom dia! Preciso auxilio para desenvolver a seguinte questão.
O domínio e imagem da relação
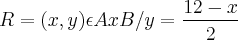
, sendo

e
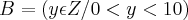
são respectivamente:
o Gabarito é D(R) = {2,4,6,8,10} e Im(R) = {1,2,3,4,5}
Grata

-
vspagnolo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Nov 25, 2013 11:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Domínio e Imagem
por dimalmeida » Seg Abr 09, 2012 11:22
- 0 Respostas
- 1164 Exibições
- Última mensagem por dimalmeida

Seg Abr 09, 2012 11:22
Funções
-
- imagem e domínio
por leticiapires52 » Sex Set 26, 2014 11:39
- 1 Respostas
- 1366 Exibições
- Última mensagem por Cleyson007

Sex Set 26, 2014 12:16
Geometria Analítica
-
- Domínio, imagem
por my2009 » Qua Mai 27, 2015 17:44
- 0 Respostas
- 2852 Exibições
- Última mensagem por my2009

Qua Mai 27, 2015 17:44
Funções
-
- Ajuda em Dominio de imagem
por Lipezyn » Seg Jun 14, 2010 20:05
- 1 Respostas
- 1511 Exibições
- Última mensagem por Molina

Seg Jun 14, 2010 21:32
Sistemas de Equações
-
- Função.imagem e dominio
por luciana correa » Seg Jul 02, 2012 21:40
- 1 Respostas
- 2288 Exibições
- Última mensagem por MarceloFantini

Seg Jul 02, 2012 23:50
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
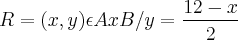 , sendo
, sendo  e
e 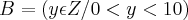 são respectivamente:
são respectivamente:

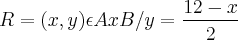 , sendo
, sendo  e
e 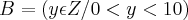 são respectivamente:
são respectivamente:


 .
.



