 por Ruan Petterson » Sex Nov 15, 2013 19:25
por Ruan Petterson » Sex Nov 15, 2013 19:25
Primeiro, para simplificar, determinei
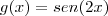
.
Segundo, determinei
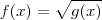
.
Bom, por via de regra

, pois não existe raiz quadrada de números negativos em

.
Portanto
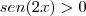
. Mas quando isso ocorre?
Vi no Wolfram|Alpha que seria quando
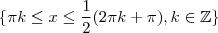
e, portanto, este seria o dominío de

.
Mas como chega-se nesse resultado? O que é o

?
Obrigado desde já!
-
Ruan Petterson
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Nov 15, 2013 19:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharela em Ciência e Tecnologia
- Andamento: cursando
 por e8group » Sex Nov 15, 2013 23:56
por e8group » Sex Nov 15, 2013 23:56
Lembre-se que a função seno é periódica de período fundamental
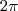

para qualquer número inteiro

.A seguir utilizaremos esta propriedade para determinar o conjunto dos pontos
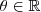
para os quais a função
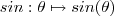
é maior ou igual a zero .
Observe inicialmente que
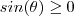
para
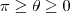
.Como ,

(k inteiro ) e
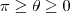
implica
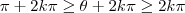
. Variando

em

obteremos uma sequência de intervalos
![... I_{-1} = [-2\pi, - \pi] , I_{0} = [0,\pi] , I_{1} = [2\pi,3\pi], .... ... I_{-1} = [-2\pi, - \pi] , I_{0} = [0,\pi] , I_{1} = [2\pi,3\pi], ....](/latexrender/pictures/80e8930ab5d6ec35fa1e513b2621e06a.png)
. Assim , concluímos
![sin\left(\bigcup_{\lambda \in \mathbb{Z}} I_\lambda \right) = [0,1] sin\left(\bigcup_{\lambda \in \mathbb{Z}} I_\lambda \right) = [0,1]](/latexrender/pictures/bf2961e5681853043bd279f9f3d9c08d.png)
.
No exercício dado , basta então tomar
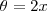
, daí segue que
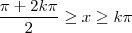
.
Portanto o domínio da função dada será
![\{\frac{\pi +2 k \pi}{2} \geq x \geq k \pi : k\in \mathbb{Z} \} = \bigcup_{k\in \mathbb{Z} } \left[\frac{\pi +2 k \pi}{2} , k\pi\right] \{\frac{\pi +2 k \pi}{2} \geq x \geq k \pi : k\in \mathbb{Z} \} = \bigcup_{k\in \mathbb{Z} } \left[\frac{\pi +2 k \pi}{2} , k\pi\right]](/latexrender/pictures/d7f1e20365fb303000d82c98f7333616.png)
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [descobrir valor para domínio] Domínio da função
por Zebra-LNX » Sáb Jun 16, 2012 12:26
- 1 Respostas
- 3250 Exibições
- Última mensagem por MarceloFantini

Ter Jun 19, 2012 22:18
Funções
-
- [Domínio] Determinar domínio a partir da função
por +danile10 » Qui Fev 07, 2013 21:33
- 1 Respostas
- 2885 Exibições
- Última mensagem por e8group

Qui Fev 07, 2013 22:38
Funções
-
- [Domínio da Função] A função abaixo é definida f(x)=x²-3x
por Tiago Neto » Qui Mai 30, 2013 20:58
- 0 Respostas
- 1770 Exibições
- Última mensagem por Tiago Neto

Qui Mai 30, 2013 20:58
Funções
-
- Integral de 6/sqrt(1-x^2) no intervalo [1/2 , sqrt(3)/2]
por Costa43 » Sex Nov 01, 2013 17:29
- 2 Respostas
- 1621 Exibições
- Última mensagem por Costa43

Dom Nov 03, 2013 13:12
Cálculo: Limites, Derivadas e Integrais
-
- dominio da funçao
por Thassya » Sex Mai 29, 2009 11:26
- 4 Respostas
- 5166 Exibições
- Última mensagem por Marcampucio

Dom Mai 31, 2009 18:58
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
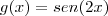 .
.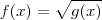 .
. , pois não existe raiz quadrada de números negativos em
, pois não existe raiz quadrada de números negativos em  .
.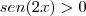 . Mas quando isso ocorre?
. Mas quando isso ocorre?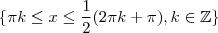 e, portanto, este seria o dominío de
e, portanto, este seria o dominío de  .
. ?
?

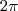
 para qualquer número inteiro
para qualquer número inteiro 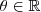 para os quais a função
para os quais a função 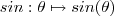 é maior ou igual a zero .
é maior ou igual a zero . 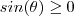 para
para 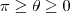 .Como ,
.Como , 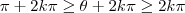 . Variando
. Variando  obteremos uma sequência de intervalos
obteremos uma sequência de intervalos ![... I_{-1} = [-2\pi, - \pi] , I_{0} = [0,\pi] , I_{1} = [2\pi,3\pi], .... ... I_{-1} = [-2\pi, - \pi] , I_{0} = [0,\pi] , I_{1} = [2\pi,3\pi], ....](/latexrender/pictures/80e8930ab5d6ec35fa1e513b2621e06a.png) . Assim , concluímos
. Assim , concluímos ![sin\left(\bigcup_{\lambda \in \mathbb{Z}} I_\lambda \right) = [0,1] sin\left(\bigcup_{\lambda \in \mathbb{Z}} I_\lambda \right) = [0,1]](/latexrender/pictures/bf2961e5681853043bd279f9f3d9c08d.png) .
.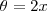 , daí segue que
, daí segue que 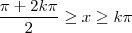 .
. ![\{\frac{\pi +2 k \pi}{2} \geq x \geq k \pi : k\in \mathbb{Z} \} = \bigcup_{k\in \mathbb{Z} } \left[\frac{\pi +2 k \pi}{2} , k\pi\right] \{\frac{\pi +2 k \pi}{2} \geq x \geq k \pi : k\in \mathbb{Z} \} = \bigcup_{k\in \mathbb{Z} } \left[\frac{\pi +2 k \pi}{2} , k\pi\right]](/latexrender/pictures/d7f1e20365fb303000d82c98f7333616.png)



 , avisa que eu resolvo.
, avisa que eu resolvo.

