Uma loja de departamentos compra cartuchos para uma determinada impressora jato de tinta a R$28,00 a unidade e prevê que, se cada cartucho for vendido a x reais, serão vendidos 200 – 2x cartuchos por mês.
a) Encontre uma fórmula que fornece o lucro mensal em função do preço de venda x de cada cartucho.
b) Estabeleça matematicamente o intervalo dos valores de x para os quais existe efetivamente lucro.
c) Para que o lucro seja máximo, qual deve ser o preço de venda x de cada cartucho?
d) Qual será o lucro máximo e quantos cartuchos serão vendidos mensalmente ao preço que maximiza esse lucro?
a)
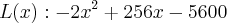
b)Para toso valor maior que zero.
c) 64 R$
d) 1296
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)