


 é um valor real e
é um valor real e 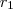 e
e 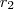 são os valores de
são os valores de  para os quais
para os quais  . Isto é, facilmente verifica-se que y(x=r_1) = y(x=r_2) = 0. Certo?
. Isto é, facilmente verifica-se que y(x=r_1) = y(x=r_2) = 0. Certo?

Russman escreveu:y(x1) = -f((4x1^2/L^2) - 1) = -f((4L^2/8^2 L^2) - 1) = -f (1-16)/16 = f(15/16)

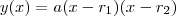
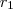 e
e 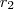 são os valores de x para os quais y=0. Isto é, facilmente verifica-se que
são os valores de x para os quais y=0. Isto é, facilmente verifica-se que  . Certo?
. Certo? você tem
você tem  , de modo que
, de modo que 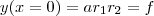 .
.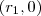 e
e 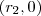 é L e ainda esses pontos são simétricos, isto é,
é L e ainda esses pontos são simétricos, isto é,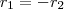 , então
, então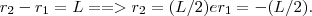
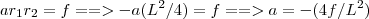
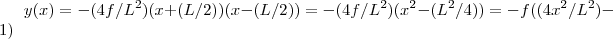
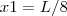 ,
, 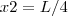 e
e 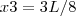 . Logo:
. Logo: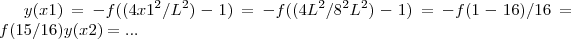

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante