Olá,
Alguém por favor poderia me ajudar a obter a inversa da função f(x)=x²-4x+3? Eu não estou conseguindo isolar o y!
Muito Obrigada!!



 em
em  .Neste contexto a função não é invertível .De fato :
.Neste contexto a função não é invertível .De fato : 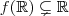 .pois ,
.pois ,  está no contradomínio da função ,entretanto
está no contradomínio da função ,entretanto 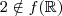 .Além disso ,
.Além disso , 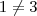 mas
mas 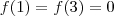 .Vamos fazer o seguinte ,suponha
.Vamos fazer o seguinte ,suponha 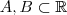 de modo que a função
de modo que a função 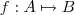 seja invertível , e sua inversa
seja invertível , e sua inversa 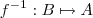 .Podemos escrever então
.Podemos escrever então 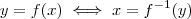 .Assim ,
.Assim , 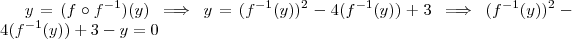 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.
 :
: