Sugiro que vc escreva as funções e aí faça a maximização:
a) Receita é dada por p.x:
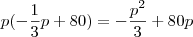
Para maximizar, vc precisa encontrar os pontos críticos e testar se é mínimo ou máximo. Pela forma da função, fica claro que será um máximo (é uma parábola côncava). Derivando e igualando a zero (ou seja, achando a função receita marginal):
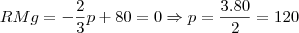
Basta resolver para p e substituir na equação de demanda:
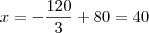
b) Lucro é RT - CT.
Basta substituir os valores de x: px - c(x) = 120.40 - 60.40-150 = 2250
c) A condição de lucro máximo é quando a RMg é igual ao CMg. Reescreva RMg em função de x.
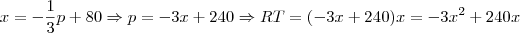

Para obter o custo marginal, da mesma forma que a receita, derive e iguale a zero a função custo. Aí basta igualar as duas funções e resolver para x:
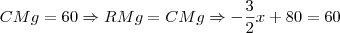
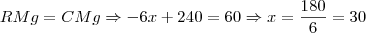
Com isso acho que dá pra concluir, certo?


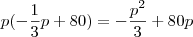
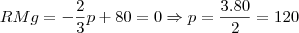
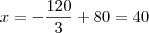
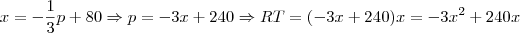

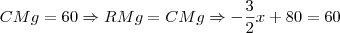
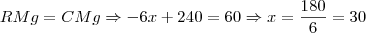

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.