 por Thiago 86 » Seg Mai 06, 2013 23:10
por Thiago 86 » Seg Mai 06, 2013 23:10
Saudações, estou estudando funções e me deparei com um beco sem saída. A questão é, saber qual é o domínio da função f(x)=
![\sqrt[2]{(x-3)(x+4)} \sqrt[2]{(x-3)(x+4)}](/latexrender/pictures/b1a4cc83a385906b64939f2432b62c47.png)
.
Eu sei que as raízes da função são x=3 e x=-4, mas não consigo raciocinar para achar o domínio que o gabarito da S={

}.
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
 por Russman » Seg Mai 06, 2013 23:51
por Russman » Seg Mai 06, 2013 23:51
Lembres-e que a raiz quadrada só se define para radicandos positivos ou o radicando nulo. Assim, voce deve estudar para quais valores de x que se verifica esse fato no radicando da função.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Thiago 86 » Qua Mai 08, 2013 22:14
por Thiago 86 » Qua Mai 08, 2013 22:14
Saudações Russman, cara eu procurei no material que eu tenho aqui em casa e não consegui encontra resposta para esse problema, tem como você dá uma explicação rápida sobre o assunto, se não for encomodo.
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
 por Russman » Qua Mai 08, 2013 22:37
por Russman » Qua Mai 08, 2013 22:37
Voce tem um funação do tipo

.
No seu caso,

.
Como a raiz quadrada só se define para valores positivos ou para o zero devemos tomar
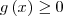
.
Assim, para estabelecer o domínio da função

voce deve calcular para qual intervalo que

. Como essa função é uma parábola de concavidade positiva, então ela será positiva a esquerda de

e a direita de

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Thiago 86 » Qua Mai 08, 2013 22:51
por Thiago 86 » Qua Mai 08, 2013 22:51
Broder muito obrigado mesmo você conseguiu resolver minhas dúvidas.

-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
 por Thiago 86 » Qui Mai 09, 2013 21:51
por Thiago 86 » Qui Mai 09, 2013 21:51
Amigão, você manja de química? Será que eu poderia postar uma questão?
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
 por Russman » Qui Mai 09, 2013 22:22
por Russman » Qui Mai 09, 2013 22:22
Depende do assunto...mas faz tempo que eu não estudo química.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função, inequação modular.
por Sugvato » Qua Abr 10, 2013 10:56
- 3 Respostas
- 1725 Exibições
- Última mensagem por Sugvato

Sex Abr 12, 2013 19:35
Funções
-
- Função e Inequação Modular
por marilgomes » Sex Mai 31, 2013 16:32
- 0 Respostas
- 818 Exibições
- Última mensagem por marilgomes

Sex Mai 31, 2013 16:32
Funções
-
- Função ( inequação do 1° grau)
por osmarioe » Seg Mai 04, 2015 13:29
- 1 Respostas
- 1249 Exibições
- Última mensagem por DanielFerreira

Qui Mai 07, 2015 23:46
Funções
-
- n sei resolver essa funçao modular com inequaçao(ajuda)
por Fabricio dalla » Qua Mar 09, 2011 23:46
- 4 Respostas
- 3274 Exibições
- Última mensagem por Renato_RJ

Sex Mar 11, 2011 15:00
Funções
-
- [INEQUAÇÂO] Inequação do tipo: (a+ x < b + x < c + x)
por Diofanto » Dom Fev 03, 2013 19:55
- 7 Respostas
- 6304 Exibições
- Última mensagem por Diofanto

Qui Fev 14, 2013 23:45
Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[2]{(x-3)(x+4)} \sqrt[2]{(x-3)(x+4)}](/latexrender/pictures/b1a4cc83a385906b64939f2432b62c47.png) .
. }.
}.
![\sqrt[2]{(x-3)(x+4)} \sqrt[2]{(x-3)(x+4)}](/latexrender/pictures/b1a4cc83a385906b64939f2432b62c47.png) .
. }.
}.


 .
. .
.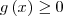 .
. voce deve calcular para qual intervalo que
voce deve calcular para qual intervalo que  . Como essa função é uma parábola de concavidade positiva, então ela será positiva a esquerda de
. Como essa função é uma parábola de concavidade positiva, então ela será positiva a esquerda de  e a direita de
e a direita de  .
.



