 por leandropressato » Sex Dez 28, 2012 09:44
por leandropressato » Sex Dez 28, 2012 09:44
Bom dia,
Tenho a seguinte função:
(f(x)-f(p)) / (x-p) .
(x diferente p) sendo f(x) = 1/x² e p= 3.
è simples substituição de formúla?
também não estou conseguindo desenvolver, se alguém puder me auxiliar nesse raciocinio.
-
leandropressato
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Dez 26, 2012 10:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bach. interd. ciencia e economia
- Andamento: cursando
 por marinalcd » Sex Dez 28, 2012 18:27
por marinalcd » Sex Dez 28, 2012 18:27
Primeiro , aconselho que utilize o editor de fórmulas, pois fica mais fácil de entendermos o exercício.
Bom, não entendi exatamente o que é proposto, seria melhor ter o enunciado junto, mas se for para fazer a substituição, basta você calcular os dados necessários a partir do que você já tem :
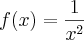
e p = 3.
Tem como calcular facilmente o que precisa e depois é só substituir.
Att.
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Russman » Sex Dez 28, 2012 21:23
por Russman » Sex Dez 28, 2012 21:23
Você precisa obter uma nova função, chamarei de

, a partir de uma

de forma que
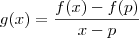
,

.
Como

, então
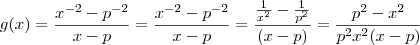
.
Simplificando,
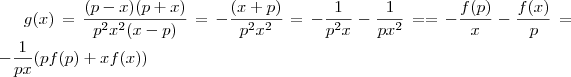
Agora basta substituir

por

...
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Sex Dez 28, 2012 21:24
por Russman » Sex Dez 28, 2012 21:24
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5573 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4589 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5745 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3484 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
-
- [FUNÇÃO] Não consigo achar a fórmula da função
por LAZAROTTI » Qui Set 27, 2012 00:06
- 1 Respostas
- 2952 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 07:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



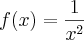 e p = 3.
e p = 3.
 , a partir de uma
, a partir de uma  de forma que
de forma que 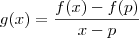 ,
,  .
. , então
, então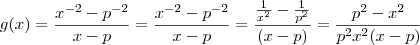 .
.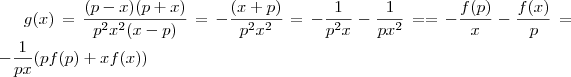
 por
por  ...
...
