É dito que uma função é par se:

E que é impar se:

Para começar, penso que a definição rezada pela maioria já tá errada, pq "é par/impar se" não faz sentido dentro do meu universo sintático, o que faz sentido para mim é "é par/impar se satisfaz a seguinte condição ou ("ou" exclusivo aqui) goza da seguinte propriedade". Sem contar que é sempre demonstrado para f(-x) e nunca para f(+x). Claro, tudo isso são "meros detalhes". Não é à toa que uma criança uma criança de 8/9 anos não é capaz de aprender "matemática de nível médio ou superior", os eruditos não são nem capazes de verbalizar linguisticamente uma simples sentença.
Enfim, agora que já fiz minhas considerações iniciais, questiono: não está errado querer enquadrar a exponencial e logarítmica nas definições acima?
As definições acima são para variações aditivas tanto em x quanto em f(x). É óbvio que a exp e a log não iriam se enquadrar, pois tais funções relacionam variações aditivas com variações multiplicativas.
Certas funções exponenciais se enquadram em:


Aqui eu omito o elemento neutro da multiplicação, se podemos omitir o da adição pq não o da multiplicação?
E certas funções logarítmicas se enquadram em:
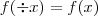

Ora, pq as funções exp e log que gozam das propriedades descritas acima não merecem o título de par ou de impar? Disserte!
Obg!

