 por Josiebruno » Seg Out 18, 2010 18:47
por Josiebruno » Seg Out 18, 2010 18:47
Oii pessoal, bom precisei pegar meu certificado na escola, e pra minha surpresa descobri que estava em dependência, no entanto tenhu dificuldade em matemática, com a ajuda de um amigo, fiz algumas questões mais, tenhu medu de naum estarem corretas , precisava de ver outros resultados.A questão é :
Construir o gráfico da função f(x)=3-2x, sendo D=[-2,5[.
-
Josiebruno
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Out 18, 2010 18:34
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Administração
- Andamento: formado
 por Marcampucio » Seg Out 18, 2010 20:52
por Marcampucio » Seg Out 18, 2010 20:52
Função do primeiro grau é uma reta. Bastam dois pontos:
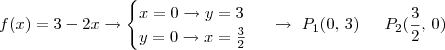

A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por MarceloFantini » Seg Out 18, 2010 21:30
por MarceloFantini » Seg Out 18, 2010 21:30
Você esqueceu de restringir o intervalo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Josiebruno » Ter Out 19, 2010 12:24
por Josiebruno » Ter Out 19, 2010 12:24
Obrigado pela ajuda.
-
Josiebruno
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Out 18, 2010 18:34
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Administração
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- gráfico
por Andreza » Qui Nov 24, 2011 13:23
- 0 Respostas
- 1511 Exibições
- Última mensagem por Andreza

Qui Nov 24, 2011 13:23
Funções
-
- Grafico
por bruno ken taniwaki » Dom Fev 24, 2013 14:36
- 0 Respostas
- 1221 Exibições
- Última mensagem por bruno ken taniwaki

Dom Fev 24, 2013 14:36
Cálculo: Limites, Derivadas e Integrais
-
- gráfico
por Jhennyfer » Seg Mai 20, 2013 08:34
- 0 Respostas
- 1214 Exibições
- Última mensagem por Jhennyfer

Seg Mai 20, 2013 08:34
Funções
-
- Gráfico com f(x)=cos.x?
por Paulo Ricardo » Qua Ago 14, 2013 03:24
- 1 Respostas
- 1773 Exibições
- Última mensagem por Russman

Qua Ago 14, 2013 21:04
Funções
-
- grafico de função
por Amparo » Dom Mar 09, 2008 20:22
- 1 Respostas
- 2572 Exibições
- Última mensagem por admin

Qui Mar 13, 2008 12:56
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


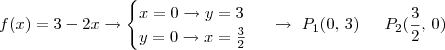






 , avisa que eu resolvo.
, avisa que eu resolvo.

