Aqui estão alguns problemas de matemática sobre função afim, por favor me ajudem na resolução!!!?
1- Verifique quais função são afins.Nelas encontre ''a" e '' b'', para f(x) igual ax+b.
A- f(x) igual 3(x +1) +4(x -1)
B- f(x) igual (x +2)elevado a 2 +(x +2)(x -2)
C- f(x) igual (x -3)elevado a 2 - x(x -5)
D- f(x) igual (x -3) -5(x -1)
2- Classifique as funções f: R (números reais) flecha indica R abaixo em afim,linear,identidade,constante e translação:
A- f(x) igual 5x+2
B- f(x) igual -x+3
C- f(x) igual 7
D- f(x) igual x
E- f(x) igual 3x
F- (f) igual x+5
3- Escreva a função afim f(x) igual ax+b, sabendo que:
A- f(1) igual 5 e f(-3) igual -7
B- f(-1) igual 7 e f(2) igual 1
4- Escreva a taxa de variação para cada uma das funções.
A- f(x) igual 4x +5
B- f(x) igual -3x +7
C- f(x) igual 3
D- f(x) igual 1/3x +2
5- Em um retângulo, o comprimento é 5 cm. Nessas condições:
A- calcule o perímetro do retângulo quando a largura for 1 cm, 1,5 cm, 2 cm, 3 cm e 4 cm,
B- construa uma tabela associando cada largura ao perímetro do retângulo,
C- se x representa a largura,qual é a lei da função que expressa o perímetro nesse retângulo?





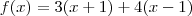

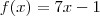
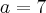 e
e 
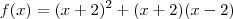

 .
.
 .
.
 :
: