 por rafacosme » Qua Jun 16, 2010 15:25
por rafacosme » Qua Jun 16, 2010 15:25
Valores de x para os quais o gráfico da função

tem tangentes horizontais são:
0, -1 e 1, alguem sabe dizer pq?
-
rafacosme
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Jun 16, 2010 15:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação ( CComp_)
- Andamento: cursando
 por Lucio Carvalho » Qua Jun 16, 2010 15:54
por Lucio Carvalho » Qua Jun 16, 2010 15:54
Olá rafacosme,
Primeiramente achamos a função derivada de f(x). Teremos:

Devemos lembrar que a primeira derivada de uma função num ponto é igual ao declive da recta tangente ao gráfico da função nesse ponto.
De acordo com o exercício, queremos descobrir os valores de x para os quais a primeira derivada é igual a zero. Então:
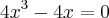
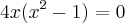

Logo,
x = 0 ou x = -1 ou x = 1
Espero ter ajudado!
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
 por rafacosme » Qua Jun 16, 2010 15:59
por rafacosme » Qua Jun 16, 2010 15:59
Obrigado Lucio!
Estou a vespera de fazer uma prova de calculo!
Valeu, entendi certinho agora
-
rafacosme
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Jun 16, 2010 15:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação ( CComp_)
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4589 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- função tangente
por leticiapires52 » Seg Out 13, 2014 10:49
- 0 Respostas
- 1085 Exibições
- Última mensagem por leticiapires52

Seg Out 13, 2014 10:49
Trigonometria
-
- Função inversa da tangente
por cristina » Ter Jun 15, 2010 13:30
- 1 Respostas
- 1389 Exibições
- Última mensagem por MarceloFantini

Ter Jun 15, 2010 20:57
Funções
-
- Cálculo I: Reta Tangente e Área da função.
por Jhonata » Ter Fev 26, 2013 12:47
- 1 Respostas
- 1441 Exibições
- Última mensagem por young_jedi

Sex Mar 01, 2013 22:22
Cálculo: Limites, Derivadas e Integrais
-
- A reta tangente ao gráfico da função (derivadas)
por Ana Maria da Silva » Dom Jun 09, 2013 21:43
- 2 Respostas
- 2074 Exibições
- Última mensagem por Ana Maria da Silva

Qua Jun 12, 2013 20:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 13 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 tem tangentes horizontais são:
tem tangentes horizontais são:
 tem tangentes horizontais são:
tem tangentes horizontais são:

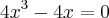
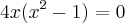




 .
.



