 por jmario » Ter Jun 08, 2010 09:13
por jmario » Ter Jun 08, 2010 09:13
Não consigo resolver essa equação
![xpx+x\sqrt[]{\frac{Px}{Py}}py=r xpx+x\sqrt[]{\frac{Px}{Py}}py=r](/latexrender/pictures/1053ab1623efff3e5736045e27daaf79.png)
porque vira
![xpx+x\sqrt[]{Px}\sqrt[]{Py}=r xpx+x\sqrt[]{Px}\sqrt[]{Py}=r](/latexrender/pictures/91118fb07125ec34e979410efa08a7c4.png)
porque some o
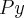
Depois eu naõ consigo fazer essa outra passagem
![y=\frac{r}{Px+\sqrt[]{Px}\sqrt[]{Py}}\sqrt[]{\frac{Px}{Py}} y=\frac{r}{Px+\sqrt[]{Px}\sqrt[]{Py}}\sqrt[]{\frac{Px}{Py}}](/latexrender/pictures/c09dc5a86f97cb309930c5b1f06d0131.png)
porque vira
![r=\frac{r}{\sqrt[]{Px}(\sqrt[]{Px}+\sqrt[]{Py)}}\sqrt[]{\frac{Px}{Py}} r=\frac{r}{\sqrt[]{Px}(\sqrt[]{Px}+\sqrt[]{Py)}}\sqrt[]{\frac{Px}{Py}}](/latexrender/pictures/2e22f58456db6ad8325c83ebaa22725f.png)
porque
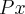
vira
![\sqrt[]{Px} \sqrt[]{Px}](/latexrender/pictures/04d8347b25aa5e75b7071bdbbbfd9071.png)
e depois no final tudo isso tem como resultado
![y=\frac{r}{Py+\sqrt[]{Px}\sqrt[]{Py}} y=\frac{r}{Py+\sqrt[]{Px}\sqrt[]{Py}}](/latexrender/pictures/c55eb258b660a5f4a6ce9d6c42f1cd56.png)
Alguém pode me ensinar as passagens, por favor?
Grato
José Mario
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7456 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
-
- Raiz quadrada
por j1a4l0 » Qui Abr 22, 2010 18:05
- 5 Respostas
- 5989 Exibições
- Última mensagem por Neperiano

Sex Abr 23, 2010 09:35
Funções
-
- raiz quadrada
por jose henrique » Seg Ago 16, 2010 16:54
- 1 Respostas
- 2348 Exibições
- Última mensagem por MarceloFantini

Ter Ago 17, 2010 00:03
Álgebra Elementar
-
- [Raiz quadrada de 13] Na mão
por Mickdark » Dom Abr 08, 2012 20:00
- 4 Respostas
- 17639 Exibições
- Última mensagem por Mickdark

Qui Abr 12, 2012 09:56
Álgebra Elementar
-
- Raiz quadrada
por anneliesero » Qua Dez 12, 2012 19:26
- 1 Respostas
- 2088 Exibições
- Última mensagem por replay

Qua Dez 19, 2012 16:11
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![xpx+x\sqrt[]{\frac{Px}{Py}}py=r xpx+x\sqrt[]{\frac{Px}{Py}}py=r](/latexrender/pictures/1053ab1623efff3e5736045e27daaf79.png)
![xpx+x\sqrt[]{Px}\sqrt[]{Py}=r xpx+x\sqrt[]{Px}\sqrt[]{Py}=r](/latexrender/pictures/91118fb07125ec34e979410efa08a7c4.png) porque some o
porque some o 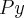
![y=\frac{r}{Px+\sqrt[]{Px}\sqrt[]{Py}}\sqrt[]{\frac{Px}{Py}} y=\frac{r}{Px+\sqrt[]{Px}\sqrt[]{Py}}\sqrt[]{\frac{Px}{Py}}](/latexrender/pictures/c09dc5a86f97cb309930c5b1f06d0131.png)
![r=\frac{r}{\sqrt[]{Px}(\sqrt[]{Px}+\sqrt[]{Py)}}\sqrt[]{\frac{Px}{Py}} r=\frac{r}{\sqrt[]{Px}(\sqrt[]{Px}+\sqrt[]{Py)}}\sqrt[]{\frac{Px}{Py}}](/latexrender/pictures/2e22f58456db6ad8325c83ebaa22725f.png)
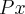 vira
vira ![\sqrt[]{Px} \sqrt[]{Px}](/latexrender/pictures/04d8347b25aa5e75b7071bdbbbfd9071.png)
![y=\frac{r}{Py+\sqrt[]{Px}\sqrt[]{Py}} y=\frac{r}{Py+\sqrt[]{Px}\sqrt[]{Py}}](/latexrender/pictures/c55eb258b660a5f4a6ce9d6c42f1cd56.png)

![xpx+x\sqrt[]{\frac{Px}{Py}}py=r xpx+x\sqrt[]{\frac{Px}{Py}}py=r](/latexrender/pictures/1053ab1623efff3e5736045e27daaf79.png)
![xpx+x\sqrt[]{Px}\sqrt[]{Py}=r xpx+x\sqrt[]{Px}\sqrt[]{Py}=r](/latexrender/pictures/91118fb07125ec34e979410efa08a7c4.png) porque some o
porque some o 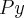
![y=\frac{r}{Px+\sqrt[]{Px}\sqrt[]{Py}}\sqrt[]{\frac{Px}{Py}} y=\frac{r}{Px+\sqrt[]{Px}\sqrt[]{Py}}\sqrt[]{\frac{Px}{Py}}](/latexrender/pictures/c09dc5a86f97cb309930c5b1f06d0131.png)
![r=\frac{r}{\sqrt[]{Px}(\sqrt[]{Px}+\sqrt[]{Py)}}\sqrt[]{\frac{Px}{Py}} r=\frac{r}{\sqrt[]{Px}(\sqrt[]{Px}+\sqrt[]{Py)}}\sqrt[]{\frac{Px}{Py}}](/latexrender/pictures/2e22f58456db6ad8325c83ebaa22725f.png)
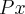 vira
vira ![\sqrt[]{Px} \sqrt[]{Px}](/latexrender/pictures/04d8347b25aa5e75b7071bdbbbfd9071.png)
![y=\frac{r}{Py+\sqrt[]{Px}\sqrt[]{Py}} y=\frac{r}{Py+\sqrt[]{Px}\sqrt[]{Py}}](/latexrender/pictures/c55eb258b660a5f4a6ce9d6c42f1cd56.png)


 .
.
 :
: