1) Ao analisar a função real definida por
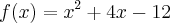 , podemos afirmar que é injetora? Justifique sua resposta.
, podemos afirmar que é injetora? Justifique sua resposta.
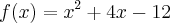 , podemos afirmar que é injetora? Justifique sua resposta.
, podemos afirmar que é injetora? Justifique sua resposta.

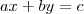 são injetoras, porque não existem duas imagens iguais para abscissas diferentes.
são injetoras, porque não existem duas imagens iguais para abscissas diferentes.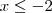 ou
ou 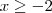 , pois -2 é o vértice da parábola, garantindo que não haja imagens iguais.
, pois -2 é o vértice da parábola, garantindo que não haja imagens iguais.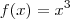 . Domínio da função:
. Domínio da função: 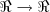 , ou seja, está definida nos reais levando nos reais. Conjunto imagem:
, ou seja, está definida nos reais levando nos reais. Conjunto imagem:  . O conjunto do contra-domínio coincide com o da imagem, e portanto ela é sobrejetora.
. O conjunto do contra-domínio coincide com o da imagem, e portanto ela é sobrejetora.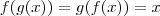 , onde
, onde  é a função identidade. Como ler isso: a composta de g com f é igual à composta de f com g que é igual à função identidade.
é a função identidade. Como ler isso: a composta de g com f é igual à composta de f com g que é igual à função identidade.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)