 por Dan » Seg Mar 08, 2010 16:21
por Dan » Seg Mar 08, 2010 16:21
Oi gente.
Me deparei com o seguinte símbolo em um texto:

Pesquisei na internet, encontrei alguns sites que falavam sobre o assunto, mas não entendi nada. Na Wikipédia há explicações sobre o uso deste símbolo (no artigo de Função), mas é realmente difícil de entender.
O texto que eu li é o seguinte:
"Uma função

(esse R é do conjunto dos reais) chama-se afim quando, para todo

o valor f(x) é dado por uma expressão do tipo f(x) = ax + b, onde a e b são constantes."
Alguém poderia me dar uma luz pra interpretar isso?
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Molina » Seg Mar 08, 2010 16:32
por Molina » Seg Mar 08, 2010 16:32
Boa tarde.
Nunca tinha parado para tentar explicar o que significa este símbolo. É uma coisa tão usual que torna-se difícil sua explicação. Mas vou tentar.
Por exemplo, numa função que se encontra

podemos dizer que é do conjunto que vamos sair para o conjunto que vamos chegar. Neste caso estamos trabalhando dos números reais para os números reais, pois numa função

utilizando valores de
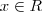
o resultado será também um número real, por isso a utilização de

(usamos números reais e obtemos um número real).
Vou dar um exemplo pobre para ver se você percebe:
Uma função

(Naturais, menos o 0

Racionais) pode ser representada por

Note que se eu substituir x por números naturais (

) irei ter um número racional (fracionário).
Espero ter ajudado.
Aguardo seu comentário!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Dan » Seg Mar 08, 2010 17:27
por Dan » Seg Mar 08, 2010 17:27
Interessante.
Podemos então dizer que uma função

é definida por
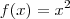
?
E como se faz a leitura disso? Eu vi em algum lugar que seria "mapeia", mas dá pra dizer simplesmente como você citou "dos números tais para os números tais"?
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Molina » Seg Mar 08, 2010 18:02
por Molina » Seg Mar 08, 2010 18:02
Isso mesmo.
Só que nesse exemplo que você deu entra em questão o 0.
Faz ou não parte dos naturais?
Quanto a leitura dele, sempre escuto os professores falar R
em R, N
em Q, R
em C, etc...

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Dan » Seg Mar 08, 2010 20:06
por Dan » Seg Mar 08, 2010 20:06
Eu sempre entendi que o zero não é um número natural, mas é escrito no conjunto.
Pois é, no que isso implica?
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Seg Mar 08, 2010 20:32
por MarceloFantini » Seg Mar 08, 2010 20:32
É um pouco confuso essa parte, existem autores que não incluem o zero nos números naturais, existem autores que incluem. Eu diria que fica a seu gosto, pois acredito que isso não influencia muito.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Dan » Seg Mar 08, 2010 22:01
por Dan » Seg Mar 08, 2010 22:01
Fantini, na maioria dos veículos de divulgação deste conteúdo, o conjunto de números naturais aparece contendo o zero. Porém, o número zero não é considerado natural por não ser utilizado em contagens (esse é um argumento). Por outro lado, o zero compartilha propriedades algébricas com outros números. Além do mais, não podemos esquecer que existe uma notação para indicar o conjunto dos naturais sem o zero que é N*.
Logo, eu me expressei de maneira a incluir o zero nos números naturais. Não sei se isso tem implicações importantes que eu não tenha notado para a operação, portanto, aguardo comentários especializados.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 (esse R é do conjunto dos reais) chama-se afim quando, para todo
(esse R é do conjunto dos reais) chama-se afim quando, para todo  o valor f(x) é dado por uma expressão do tipo f(x) = ax + b, onde a e b são constantes."
o valor f(x) é dado por uma expressão do tipo f(x) = ax + b, onde a e b são constantes."

 podemos dizer que é do conjunto que vamos sair para o conjunto que vamos chegar. Neste caso estamos trabalhando dos números reais para os números reais, pois numa função
podemos dizer que é do conjunto que vamos sair para o conjunto que vamos chegar. Neste caso estamos trabalhando dos números reais para os números reais, pois numa função  utilizando valores de
utilizando valores de 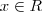 o resultado será também um número real, por isso a utilização de
o resultado será também um número real, por isso a utilização de  (Naturais, menos o 0
(Naturais, menos o 0  Racionais) pode ser representada por
Racionais) pode ser representada por 
 ) irei ter um número racional (fracionário).
) irei ter um número racional (fracionário).

 é definida por
é definida por 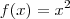 ?
?


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.