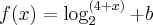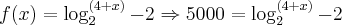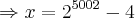por bryelfc » Qua Mai 25, 2016 13:20
por bryelfc » Qua Mai 25, 2016 13:20
Sabe-se que a produção de cestos de uma comunidade indígena é comercializada por uma cooperativa, cujo lucro, em milhares de reais, resultante da venda da produção de x unidades, é estimado pela função f(x) = log2(4 + x) + b , sendo b uma constante real, e que não havendo produção não haverá lucro.
Com base nessa informação, determine o lucro médio na produção de cada unidade quando o lucro for igual a R$5000,00.
-
bryelfc
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Mai 25, 2016 13:11
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por nakagumahissao » Qui Mai 26, 2016 02:24
por nakagumahissao » Qui Mai 26, 2016 02:24
Sabe-se que a produção de cestos de uma comunidade indígena é comercializada por uma cooperativa, cujo lucro, em milhares de reais, resultante da venda da produção de x unidades, é estimado pela função f(x) = log2(4 + x) + b , sendo b uma constante real, e que não havendo produção não haverá lucro.
Com base nessa informação, determine o lucro médio na produção de cada unidade quando o lucro for igual a R$5000,00.
Sendo que b é uma constante real e que não havendo produção não haverá lucro, então:
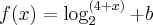

Logo:

Para se ter um lucro de R$ 5.000,00 teremos:
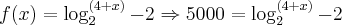

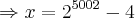
Esta resposta é muito estranha. Me dá a impressão que a questão está formulada de forma errada ou houve erro de digitação. De qualquer forma, este resultado diz que para se ter um lucro de 5000 reais, seriam necessários a produção de um número elevadíssimo de cestas (várias vidas de várias pessoas para se obter toda essa produção?), por isso causa estranheza.
O lucro médio será:


Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por bryelfc » Qui Mai 26, 2016 02:48
por bryelfc » Qui Mai 26, 2016 02:48
Pow nem fala cara, bati muito a cabeça achando que eu tava errando alguma coisa. A prova é da bahiana de medicina aqui em Salvador, e essa faculdade tem cada questão bizarra na fase aberta. No mais valeu, seu resultado bateu com o meu
-
bryelfc
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Mai 25, 2016 13:11
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função Exponencial] Questão 25 da Bahiana de Medicina 2013
por Bruno Hitner » Ter Abr 02, 2013 00:47
- 4 Respostas
- 3523 Exibições
- Última mensagem por Bruno Hitner

Dom Abr 07, 2013 01:09
Funções
-
- Função Logarítmica
por OtavioBonassi » Qui Jan 06, 2011 21:58
- 12 Respostas
- 7985 Exibições
- Última mensagem por OtavioBonassi

Sex Jan 07, 2011 23:42
Funções
-
- Função Logaritmica
por nessitahfl » Qui Abr 17, 2014 11:06
- 3 Respostas
- 2570 Exibições
- Última mensagem por nessitahfl

Ter Abr 22, 2014 10:48
Funções
-
- Função Logarítmica
por Carlos28 » Sex Mar 13, 2015 10:02
- 2 Respostas
- 2456 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:36
Logaritmos
-
- Função logarítmica
por zenildo » Qua Jul 15, 2015 12:26
- 1 Respostas
- 2047 Exibições
- Última mensagem por nakagumahissao

Qui Jul 16, 2015 14:37
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.