como montar está função ?
O valor da conta de um celular é dado por uma tarifa fixa,mais uma parte que varia de acordo com o consumo em minutos.A tabela a seguir, fornece os valores dessa conta nos quatro últimos meses e os respectivos números de ligações:
CONSUMO (min 0) = 36 52 A 70
CUSTO (R$) = 33,4 35,8 37,15 B
Com base nesses dados: estabeleça a função C(t)=at+b que relaciona o custo C,contado em reais,com o consumo t,medido em minutos, da conta relativa a certo mês?
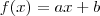que passa pelos pontos 
e 
.
e 
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)