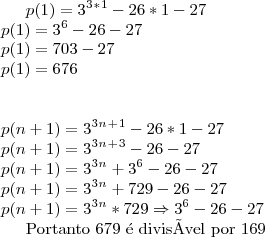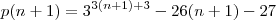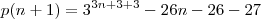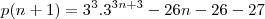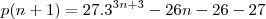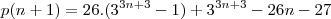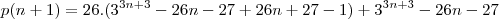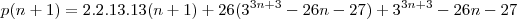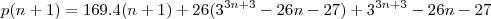por juliohenriquelima14 » Sáb Dez 13, 2014 19:03
por juliohenriquelima14 » Sáb Dez 13, 2014 19:03
Boa tarde !
Pessoal estou com muita dificuldade para resolver essa questão.
1- Mostre por indução que para todo
n pertencente ao conjunto dos números naturais

Envolve divisibilidade, tenho que provar que

é divisivel por 169.
Agradeço desde já a atenção de vocês.
-
juliohenriquelima14
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Nov 01, 2014 09:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema da Informação
- Andamento: cursando
 por juliohenriquelima14 » Sáb Dez 13, 2014 21:24
por juliohenriquelima14 » Sáb Dez 13, 2014 21:24
juliohenriquelima14 escreveu:Boa tarde !
Pessoal estou com muita dificuldade para resolver essa questão.
1- Mostre por indução que para todo
n pertencente ao conjunto dos números naturais

Consegui fazer o seguinte, alguém corrige?
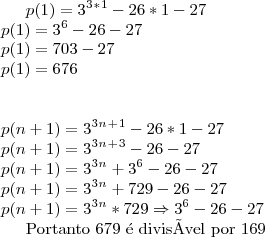
-
juliohenriquelima14
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Nov 01, 2014 09:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema da Informação
- Andamento: cursando
 por young_jedi » Sáb Dez 13, 2014 21:44
por young_jedi » Sáb Dez 13, 2014 21:44
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por juliohenriquelima14 » Sáb Dez 13, 2014 23:27
por juliohenriquelima14 » Sáb Dez 13, 2014 23:27
Boa noite meu caro!
Muito agradecido por disponibilizar um pouco do seu tempo p corrigir meu erro.
Obrigado!
-
juliohenriquelima14
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Nov 01, 2014 09:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema da Informação
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Não consigo resolver essa questão com derivada
por Cristiano Tavares » Sáb Jun 18, 2011 12:18
- 2 Respostas
- 1836 Exibições
- Última mensagem por Cristiano Tavares

Sáb Jun 18, 2011 15:07
Cálculo: Limites, Derivadas e Integrais
-
- Quádricas não consigo desenvolver essa questão
por berg_nascimento » Qui Jun 30, 2016 14:58
- 0 Respostas
- 1462 Exibições
- Última mensagem por berg_nascimento

Qui Jun 30, 2016 14:58
Geometria Analítica
-
- P.A nao consigo resolver essa p.a.
por Dalila » Sex Nov 14, 2008 16:58
- 2 Respostas
- 3134 Exibições
- Última mensagem por admin

Sex Nov 14, 2008 17:29
Progressões
-
- Não consigo resolver essa integral
por Cristiano Tavares » Qua Mai 11, 2011 22:16
- 2 Respostas
- 2078 Exibições
- Última mensagem por Cristiano Tavares

Qua Mai 11, 2011 23:59
Cálculo: Limites, Derivadas e Integrais
-
- Não consigo calcular essa derivada!!!
por Catalao » Qua Mai 09, 2012 19:51
- 3 Respostas
- 2374 Exibições
- Última mensagem por LuizAquino

Seg Mai 14, 2012 14:55
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 é divisivel por 169.
é divisivel por 169.