
O Problema é o seguinte:
A equação da superfície de uma montanha é:
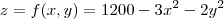
onde as distâncias são medidas em metros.
Suponha que os pontos do eixo positivo de x estão a leste, e os pontos do eixo positivo de y ao norte.
Suponha também que um alpinista está no ponto
 .
.a) Qual é a direção da parte que tem a inclinação mais acentuada?
Calculei o
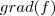 no ponto dado e pela fórmula de derivadas direcionais, deduzi que a direção seria oposta ao do gradiente.
no ponto dado e pela fórmula de derivadas direcionais, deduzi que a direção seria oposta ao do gradiente.O gradiente deu (60,-20). A direção seria oposta a desse vetor.
b) Se o alpinista se mover na direção leste, ele estará subindo ou descendo? Qual é a sua velocidade?
Fiz a derivada direcional na direção
 Pra achar a velocidade.
Pra achar a velocidade. Pela resposta anterior, ele estaria subindo, com V=60 m/u.t
c) Em que direção ele estará percorrendo um caminho plano?
Eu nem sei como fazer essa. Acho que deve ter algo a ver com a curva de nível em que o alpinista estaria, que é

Mas como achar a direção?
Obrigado, desculpem se ficou grande




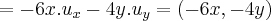
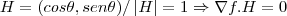 ,tomara a direçao de maior crescimento,e claro maior inclinaçao da montanha...logo
,tomara a direçao de maior crescimento,e claro maior inclinaçao da montanha...logo 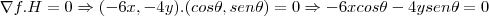 ...
...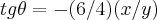
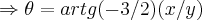 ,se tomarmos x,y dos vetores (1,0),(0,1),entao
,se tomarmos x,y dos vetores (1,0),(0,1),entao 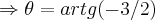 ,
,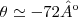 ,q. sera um ponto a noroeste do sistema...se tomarmos os pontos(-10,5)
,q. sera um ponto a noroeste do sistema...se tomarmos os pontos(-10,5) nordeste do sistema...
nordeste do sistema...![v=\left|\nabla f(-10,5) \right|=\left|(60,20) \right|=\sqrt[]{({60})^{2}+(({-20})^{2}} v=\left|\nabla f(-10,5) \right|=\left|(60,20) \right|=\sqrt[]{({60})^{2}+(({-20})^{2}}](/latexrender/pictures/49aab0979b30ad92f86e2ec94b5b263d.png)
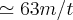

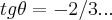 em relaçao a base da montanha,onde podemos tomar os vetores (1,0),(0,1)
em relaçao a base da montanha,onde podemos tomar os vetores (1,0),(0,1) ,a direçao do gradiente estara no terceiro e quarto quadrantes do sistema proposto,e como calculamos
,a direçao do gradiente estara no terceiro e quarto quadrantes do sistema proposto,e como calculamos 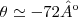 (direçao sudeste) e tambem(esqueci de colocar (
(direçao sudeste) e tambem(esqueci de colocar ( direçao noroeste...entao a montanha "cresce" nas direçoes sudeste(-72º)e noroeste(108º)do sistema...
direçao noroeste...entao a montanha "cresce" nas direçoes sudeste(-72º)e noroeste(108º)do sistema...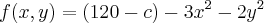 ,onde c sera uma curva de nivel da montanha,e onde o vetor gradiente e perpendicular ao vetor unitario do gradiente de f(x,y),ou seja
,onde c sera uma curva de nivel da montanha,e onde o vetor gradiente e perpendicular ao vetor unitario do gradiente de f(x,y),ou seja 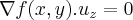 ,onde
,onde ![{u}_{z}=(6/\sqrt[]{52},4/\sqrt[]{52}) {u}_{z}=(6/\sqrt[]{52},4/\sqrt[]{52})](/latexrender/pictures/53dce05991aaf1eccf275a1a6fab9173.png) ...
...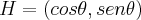 e tal q.
e tal q. ![\left|H \right|=\sqrt[]{{cos\theta}^{2}+{sen\theta}^{2}}=1 \left|H \right|=\sqrt[]{{cos\theta}^{2}+{sen\theta}^{2}}=1](/latexrender/pictures/50e9cca57ef6d58cb7eaa27f75408856.png) ,H e um vetor q. busca uma direçao(um angulo
,H e um vetor q. busca uma direçao(um angulo  no sistema de coordenadas)e uma maneira de encontrar a direçao do gradiente,qdo o gradiente e o vetor unitario do gradiente alinham-se,entao e a direçao de maior crescimento...
no sistema de coordenadas)e uma maneira de encontrar a direçao do gradiente,qdo o gradiente e o vetor unitario do gradiente alinham-se,entao e a direçao de maior crescimento... em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.