cacule lim(n+7/n+5)^raiz quadrada de n
? ? ?
? ?
? ? ?



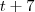 difere apenas de
difere apenas de  por uma constante real positiva 2 , a nossa intuição diz que lá no infinito às retas
por uma constante real positiva 2 , a nossa intuição diz que lá no infinito às retas  que por sua vez são paralelas se " encontram no infinito e segue -se continuamente uma tangenciando a outra " .
que por sua vez são paralelas se " encontram no infinito e segue -se continuamente uma tangenciando a outra " .  expectativa :
expectativa : 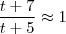 sempre que
sempre que  para algum
para algum  dado .
dado . 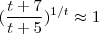 o que nos leva diz que o limite é 1 . E de fato a nossa expectativa se confirma .
o que nos leva diz que o limite é 1 . E de fato a nossa expectativa se confirma . o que implica que
o que implica que 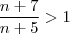 ( já que
( já que  no contexto és natural (diferente de t , ex. acima) ) que possua vez implica
no contexto és natural (diferente de t , ex. acima) ) que possua vez implica  e ainda
e ainda 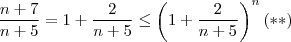 (já que
(já que 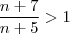 ) de forma equivalente
) de forma equivalente  . Logo , formalmente obtemos ,
. Logo , formalmente obtemos , 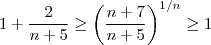 .Quando
.Quando 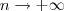 , o teorema do confronto valida nossa intuição .
, o teorema do confronto valida nossa intuição .
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)