




 uma função real .
uma função real .  é decrescente se para todo
é decrescente se para todo  do domínio de
do domínio de  implica
implica 
 é crescente se para todo
é crescente se para todo  do domínio de
do domínio de  implica
implica 
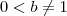 e definiremos f por
e definiremos f por  .
. .
.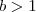 . Daí se
. Daí se  implica
implica 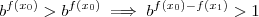 . Como
. Como 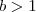 então ,
então ,  somente se
somente se  o que mostra que
o que mostra que 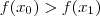 . Acabamos de mostrar que
. Acabamos de mostrar que 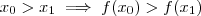 ;logo
;logo  é estritamente crescente .
é estritamente crescente .  , agora avalie
, agora avalie 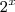 para valores positivos e negativos de
para valores positivos e negativos de  .
. 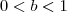 , fazendo as mesmas contas vamos chegar em
, fazendo as mesmas contas vamos chegar em  .Como
.Como 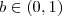 então
então  se o expoente for negativo , daí
se o expoente for negativo , daí  . Acabamos de mostrar que
. Acabamos de mostrar que 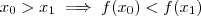 ; logo
; logo  é estritamente decrescente .
é estritamente decrescente . ,
, 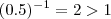 e
e  .
.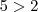 e
e 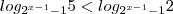 . Pela teoria acima , devemos ter
. Pela teoria acima , devemos ter 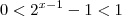 .
.
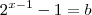 . Daí, sabemos que o logaritmo de 5 nessa base é menor que o de 2 nessa mesma base. Essa é a informação do problema!
. Daí, sabemos que o logaritmo de 5 nessa base é menor que o de 2 nessa mesma base. Essa é a informação do problema!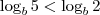
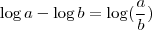 . Assim, voltando a relação do exercício,
. Assim, voltando a relação do exercício,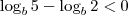
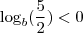
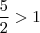 . E agora? Será q não tem solução? A informação que está ausente no que se aprende no colégio é: o log pode ser negativo mesmo que o "logaritmando" seja maior que 1 desde que a BASE a qual ele está sendo calculado seja menor que 1. Está aí nosso detalhe.
. E agora? Será q não tem solução? A informação que está ausente no que se aprende no colégio é: o log pode ser negativo mesmo que o "logaritmando" seja maior que 1 desde que a BASE a qual ele está sendo calculado seja menor que 1. Está aí nosso detalhe.  e
e  . Por hipótese, tomemos
. Por hipótese, tomemos  e
e  de modo que
de modo que 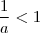 . ( Você concorda com isso? Se não, é só testar: 1/10<1, 1/25<1, 1/2 <1,...). Agora, suponhamos que os números se relacionem da seguinte forma:
. ( Você concorda com isso? Se não, é só testar: 1/10<1, 1/25<1, 1/2 <1,...). Agora, suponhamos que os números se relacionem da seguinte forma:
 , então deve ser verdade que
, então deve ser verdade que 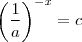 .
.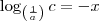 .
.

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)