Mais uma vez precisando da ajuda de vocês!
Determine o domínio das seguintes funções:
1)
![f(x)=\frac{1}{\sqrt[]{9-{x}^{2}}} f(x)=\frac{1}{\sqrt[]{9-{x}^{2}}}](/latexrender/pictures/2ca0cc4c086c319df690d96cabd60891.png)
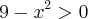
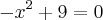
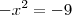
![x=\sqrt[]{9} x=\sqrt[]{9}](/latexrender/pictures/e3bba98047539d564c787e8b39fbef97.png)
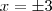


2)
![f(x)= \frac{\sqrt[]{{x}^{2}+x}}{{x}^{2}+x} f(x)= \frac{\sqrt[]{{x}^{2}+x}}{{x}^{2}+x}](/latexrender/pictures/57d12ed478b1ca4cff834f7d003fce23.png)
Gabarito:
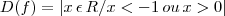
Obs.:Não sei como resolver esta última questão, como o denominador tem que ser
 0, não estou sabendo esboçar o gráfico!
0, não estou sabendo esboçar o gráfico! 
Gostaria de saber se a primeira está correta (não tenho gabarito) e também como fazer a segunda incluindo o gráfico!
Desde já agradeço a colaboração!



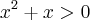 , porém eu fiz
, porém eu fiz  !
!
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)