1.Resolva a seguinte inequação:
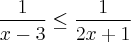
Resolução:
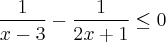
Tirando o m.m.c dos denominadores:

Achando as Raízes:
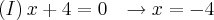

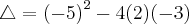
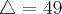
>>>Bhaskara:
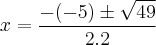


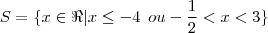
Gostaria que algum amigo mais safo em matemática, verificasse se minha resolução está correta (principalmente o estudo de sinais)!
obs.: Não tenho o gabarito!
Desde já agradeço a colaboração!


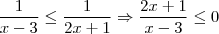 .
.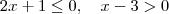 ( aqui,
( aqui,  não pode ser
não pode ser  )
)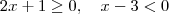
 pois é raiz do denominador da equação original como
pois é raiz do denominador da equação original como  .
.
 e verifique se vale a relação que você afirmou.
e verifique se vale a relação que você afirmou. e
e  já declaram os valores em que
já declaram os valores em que 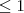 " na inequação! hahah Falta de atenção.
" na inequação! hahah Falta de atenção.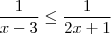 ?
?![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)