 por Sobreira » Ter Fev 25, 2014 08:51
por Sobreira » Ter Fev 25, 2014 08:51
Prezados,
Estava estudando alguns gráficos de funções e estava com uma dificuldade.
Algumas funções possuem gráficos característicos, como a exponencial, segundo grau etc.
Minha dúvida é a seguinte:
As vezes vemos uma função e tentamos já imaginar o gráfico da função mas ele é diferente do imaginado pois a função, digamos, não é puramente exponencial, segundo grau etc.
Por exemplo:

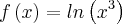
Nestes casos por exemplo, o gráfico foge do tradicional, tanto da exponencial quanto do logaritmo.
A minha dúvida é:
Se eu olhar para uma função e ela não for puramente exponencial, logaritmica, etc já não posso fazer aquela imagem do gráfico na minha cabeça??
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Bravim » Ter Fev 25, 2014 23:50
por Bravim » Ter Fev 25, 2014 23:50
Eu acho que particulamente é importante pensar como se fosse cada uma separadamente. Desse jeito fica mais fácil de visualizar para mim, mas pode ser que talvez seja melhor pensar nessas funções através de algumas substituições como por exemplo:
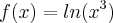
faz-se
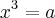
e talvez fique mais fácil de ver a cara da função...
Derivando também é um bom jeito de verificar a "cara" da função, bem como calculando limites em alguns pontos.
Espero ter ajudado

-

Bravim
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Qui Out 03, 2013 03:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- funções e gráficos
 por ezidia51 » Sex Ago 24, 2018 01:21
por ezidia51 » Sex Ago 24, 2018 01:21
- 4 Respostas
- 7350 Exibições
- Última mensagem por ezidia51

Sex Ago 24, 2018 18:58
Funções
-
- Funções e gráficos
por Fernandobertolaccini » Sex Jun 06, 2014 11:28
- 0 Respostas
- 1284 Exibições
- Última mensagem por Fernandobertolaccini

Sex Jun 06, 2014 11:28
Funções
-
- Gráficos e funçoes
por Neydimara » Ter Ago 05, 2014 19:41
- 0 Respostas
- 1242 Exibições
- Última mensagem por Neydimara

Ter Ago 05, 2014 19:41
Geometria Analítica
-
- Graficos que representam funções.
por ibatexano » Ter Out 06, 2009 13:36
- 1 Respostas
- 2287 Exibições
- Última mensagem por ibatexano

Ter Out 06, 2009 14:26
Funções
-
- Graficos estatisticos e Funcoes
por j_cruz » Qui Fev 11, 2010 18:16
- 1 Respostas
- 2897 Exibições
- Última mensagem por Molina

Qui Fev 11, 2010 21:36
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

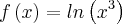


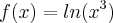
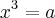 e talvez fique mais fácil de ver a cara da função...
e talvez fique mais fácil de ver a cara da função... 







