 por felipemreis » Sex Set 13, 2013 13:29
por felipemreis » Sex Set 13, 2013 13:29
Estou com dúvida na seguinte questão:

Mostre que f é função de 1 grau:
a)f(x)= (x-6)^2-(x-3)*(x-6)
b)f(x)= 2x^3+2x/3x^2+3
EU TENTEI RESOLVER OS POLINÔMIOS DE CADA FUNÇÃO, MAS EU NÃO CONSEGUI CHEGAR A UMA RESPOSTA COERENTE!
NÃO SEI COMO RESOLVER, POR FAVOR ME AJUDEM!

- Essa é a imagem da questão que eu escanei do livro, mostra a questão.
-
felipemreis
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Set 13, 2013 13:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por temujin » Sex Set 13, 2013 15:22
por temujin » Sex Set 13, 2013 15:22
Olá.
Procure colocar sempre uma questão por tópico. Aumenta as chances de que alguém responda sua dúvida. Vamos lá:
a)
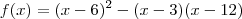
Desenvolva os polinômios:
![f(x) = [x^2-12x+36]-[x^2-15x+72] = 3x-36 f(x) = [x^2-12x+36]-[x^2-15x+72] = 3x-36](/latexrender/pictures/e73d57121e5f0f5ed63dd26893f7577d.png)
Onde a segunda parte é obtida apenas aplicando a distributiva.
b)
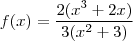
Aqui vc pode começar pensando em fatorar os polinômios. Veja que tanto no numerador quanto no denominador vc tem alguma coisa em comum entre os termos. No numerador 2x aparece em cada um dos termos e no caso do denominador 3 aparece em cada um dos termos, então comece por aí.
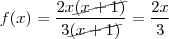
-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
 por Russman » Sex Set 13, 2013 17:40
por Russman » Sex Set 13, 2013 17:40
Na letra b) suponha que
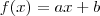
. Assim,
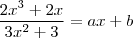
donde
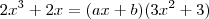
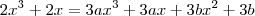
Daí, por igualdade de polinômios, temos
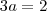
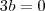
Logo,
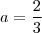
e

. De fato, a função é de 1° grau e
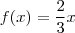
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por felipemreis » Sex Set 13, 2013 19:56
por felipemreis » Sex Set 13, 2013 19:56
Obrigado! temujin. Esclareceu as minhas dúvidas. Mas segundo o livro a resposta correta da letra a é: f(x)=3x. Foi diferente da sua resposta!
-
felipemreis
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Set 13, 2013 13:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por temujin » Sex Set 13, 2013 19:59
por temujin » Sex Set 13, 2013 19:59
felipemreis escreveu:Obrigado! temujin. Esclareceu as minhas dúvidas. Mas segundo o livro a resposta correta da letra a é: f(x)=3x. Foi diferente da sua resposta!
Claro, engano meu. Veja que o produto do segundo termo é 3.12 = 36

-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
 por felipemreis » Sáb Set 14, 2013 01:13
por felipemreis » Sáb Set 14, 2013 01:13
-
felipemreis
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Set 13, 2013 13:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função] isso é função do segundo grau?
por maulakalanata » Qua Mar 27, 2013 04:03
- 1 Respostas
- 2281 Exibições
- Última mensagem por timoteo

Qua Mar 27, 2013 10:51
Funções
-
- [Função 1°grau] determinar função.
por Thiago 86 » Ter Abr 23, 2013 11:27
- 2 Respostas
- 2409 Exibições
- Última mensagem por Thiago 86

Ter Abr 23, 2013 13:05
Funções
-
- Função do 2° Grau
por mimi2009 » Qua Jun 10, 2009 05:46
- 1 Respostas
- 2087 Exibições
- Última mensagem por Molina

Qua Jun 10, 2009 08:05
Funções
-
- Função do 2 grau...
por Fiel8 » Qua Jul 01, 2009 21:34
- 4 Respostas
- 3440 Exibições
- Última mensagem por Cleyson007

Qui Jul 02, 2009 16:16
Funções
-
- Função 1° grau
por DanielFerreira » Ter Set 22, 2009 14:14
- 2 Respostas
- 2138 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 19:06
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


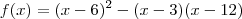
![f(x) = [x^2-12x+36]-[x^2-15x+72] = 3x-36 f(x) = [x^2-12x+36]-[x^2-15x+72] = 3x-36](/latexrender/pictures/e73d57121e5f0f5ed63dd26893f7577d.png)
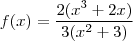
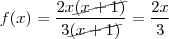

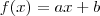 . Assim,
. Assim,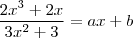
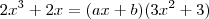
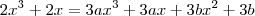
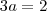
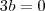
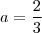 e
e  . De fato, a função é de 1° grau e
. De fato, a função é de 1° grau e 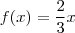 .
.




![(x-6)^2 = [x^2-12x+36] (x-6)^2 = [x^2-12x+36]](/latexrender/pictures/c259c876cbbaa9ddf2cd238b5fd1c7c1.png)
![(x-3)(x-12)=[x^2-15x+36] (x-3)(x-12)=[x^2-15x+36]](/latexrender/pictures/a81e963d2a6bb1115f49de764052eff1.png)
![f(x) = [x^2-12x+36]-[x^2-15x+36] = 3x f(x) = [x^2-12x+36]-[x^2-15x+36] = 3x](/latexrender/pictures/1611066d30e3283b36437ce479dc36f6.png)










