 por virginia » Sex Abr 26, 2013 14:09
por virginia » Sex Abr 26, 2013 14:09
Boa tarde segue abaixo outro exercício que não consegui resolver.
Determinar todos os intervalos de números que satisfaçam a desigualdade.
X³ +1> X² + X
Bom comecei assim

> 0
Logo x³+1 #0 sendo x # - 1
Não conseguir fazer mais nada e a resposta do livro é:(-1,1)U(1, +infinito).
Obrigada.
-
virginia
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Jul 12, 2012 15:15
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Administração
- Andamento: formado
 por e8group » Sex Abr 26, 2013 17:25
por e8group » Sex Abr 26, 2013 17:25
Infelizmente não podemos proceder como vc fez .
Pense um pouco :
Claramente
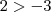
, mas
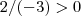
é um absurdo .Desta forma ,não necessariamente
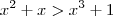
implica
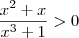
(Por quê ?) .
Mas ,note que se
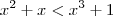
então
![x^2 + x -[x^3 + 1] < x^3 + 1 -[x^3 + 1] = 0 x^2 + x -[x^3 + 1] < x^3 + 1 -[x^3 + 1] = 0](/latexrender/pictures/c267e0702fc8dfac0b0c0b0db98e34e1.png)
. Logo ,
se
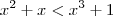
concluímos que

.
Agora observe que o número 1 é solução da equação

.Assim ,podemos fatorar

ao dividir por

obtendo ... . Aliás ,pensando melhor ,
note que
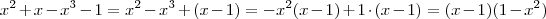
.
E ainda
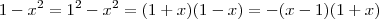
.
Daí
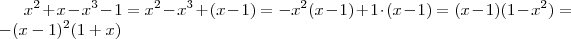
.
Agora é fácil , como

é sempre positivo para todo

,concluímos que
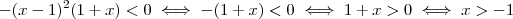
.Lembrando que

segue a reposta do gabarito .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Intervalos
por Revelants » Dom Out 05, 2008 15:02
- 1 Respostas
- 2165 Exibições
- Última mensagem por Molina

Dom Out 05, 2008 15:43
Funções
-
- Intervalos de confiança
por miguel337 » Seg Jul 18, 2011 12:34
- 1 Respostas
- 6653 Exibições
- Última mensagem por Neperiano

Seg Jul 18, 2011 20:39
Estatística
-
- [Intervalos] me ajudem
por suhkaiser » Qui Mai 17, 2012 15:57
- 1 Respostas
- 1087 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 19, 2012 09:11
Funções
-
- União de intervalos.
por eu_dick1 » Sex Mai 23, 2014 14:16
- 4 Respostas
- 3420 Exibições
- Última mensagem por alienante

Sáb Mai 24, 2014 21:09
Conjuntos
-
- Limite- Continuidade em intervalos
por killerkill » Sáb Ago 13, 2011 02:25
- 7 Respostas
- 7927 Exibições
- Última mensagem por killerkill

Qua Ago 17, 2011 23:17
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 > 0
> 0
 > 0
> 0
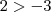 , mas
, mas 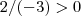 é um absurdo .Desta forma ,não necessariamente
é um absurdo .Desta forma ,não necessariamente 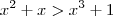 implica
implica 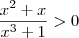 (Por quê ?) .
(Por quê ?) . 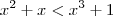 então
então ![x^2 + x -[x^3 + 1] < x^3 + 1 -[x^3 + 1] = 0 x^2 + x -[x^3 + 1] < x^3 + 1 -[x^3 + 1] = 0](/latexrender/pictures/c267e0702fc8dfac0b0c0b0db98e34e1.png) . Logo ,
. Logo , 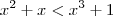 concluímos que
concluímos que  .
.  .Assim ,podemos fatorar
.Assim ,podemos fatorar  ao dividir por
ao dividir por  obtendo ... . Aliás ,pensando melhor ,
obtendo ... . Aliás ,pensando melhor ,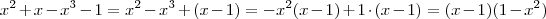 .
. 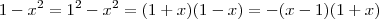 .
. 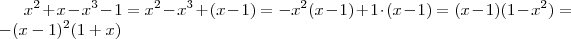 .
. é sempre positivo para todo
é sempre positivo para todo  ,concluímos que
,concluímos que 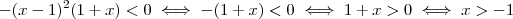 .Lembrando que
.Lembrando que  segue a reposta do gabarito .
segue a reposta do gabarito .

 .
.



