Por favor sempre utilize LaTeX para redigir suas expressões.Além disso ,seria importante postar apenas uma dúvida por tópico .
Observe o código e o resultado [(1),(2)]:
- Código: Selecionar todos
\lim_{x\to 0} \frac{\sqrt{16-x} - 4 }{x}
(1)
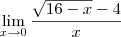
- Código: Selecionar todos
\lim_{h\to 0} \frac{(a+h)^3 - a^3 }{h}
(2)
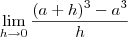
Resolução :
Em (1) ,basta multiplicar o numerador e o denominador por

. Fazendo as devidas simplificações e calculando o limite encontrará a resposta desejada .(Observe
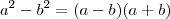
e também
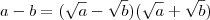
neste caso desde que
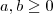
,no outro não há restrição )
Em(2) ,uma das possíveis formas de solução é considerar
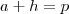
.Assim , quando
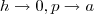
.
Deste modo, este limite é equivalente a
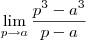
.
Mas ,

pode ser fatorado ,isto é ,
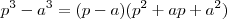
.
Então ,
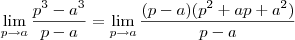
,visto que
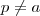
,ou seja,
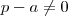
podemos simplificar a expressão acima ,obtendo
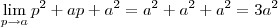
.
Portanto , podemos dizer que
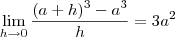
.


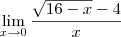
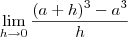
 . Fazendo as devidas simplificações e calculando o limite encontrará a resposta desejada .(Observe
. Fazendo as devidas simplificações e calculando o limite encontrará a resposta desejada .(Observe 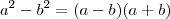 e também
e também 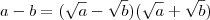 neste caso desde que
neste caso desde que 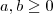 ,no outro não há restrição )
,no outro não há restrição )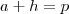 .Assim , quando
.Assim , quando 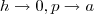 .
.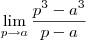 .
.  pode ser fatorado ,isto é ,
pode ser fatorado ,isto é , 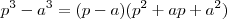 .
. 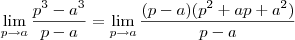 ,visto que
,visto que 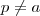 ,ou seja,
,ou seja, 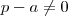 podemos simplificar a expressão acima ,obtendo
podemos simplificar a expressão acima ,obtendo 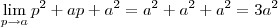 .
. 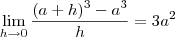 .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

