Essa questão eu resolvi por inspeção. Gostaria de ver as opções de resolução que vocês sugerem. Achei bem interessante.



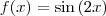 ) atinge seu máximo em 1 e mínimo em menos 1.
) atinge seu máximo em 1 e mínimo em menos 1.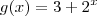 .
.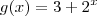 neste intervalo, mas para quais valores de
neste intervalo, mas para quais valores de  ?
?
 que satisfaça nenhuma das desigualdades (pelo menos valores em
que satisfaça nenhuma das desigualdades (pelo menos valores em  ).
).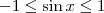 ;
; e a função logaritmo (e a seno também) é sempre continua o que força que se cruzem em algum lugar.
e a função logaritmo (e a seno também) é sempre continua o que força que se cruzem em algum lugar.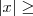 , indicando que se interceptarão no zero pelo menos.
, indicando que se interceptarão no zero pelo menos.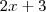 é o mesmo caso de
é o mesmo caso de  .
.



Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

