 por SILMARAKNETSCH » Qua Nov 14, 2012 18:21
por SILMARAKNETSCH » Qua Nov 14, 2012 18:21
vejam quanto importantes foram os colegas para meus estudos, comecei sem saber aplicar sequer a entrada da formula e voces me ensinaram a fazer pelo editor de fórmulas levei alguns dias mas com a benevolência dos colegas me deram um conhecimento pro resto da minha vida, ainda continuo apanhando com limites, derivadas mas faltam tres modelos para aprender e enviei uma matéria ao meu professor de como eu estava aprendendo citando o site ele aceitou minha lição de casa feita num sulfite a caneta por não saber usar os programas de formatação e mesmo assim eu dizendo que vcs estavam me ajudando que não resolvi os problemas sózinha deu-me as notas da tarefa que se chama portifólio é para ensino EAD a distância pois sou deficiente física e disse que assim mesmo me daria a nota por estar procurando aprender e agradeço a todos os voluntários porque vcs é que me deram a chance de tirar nota e aprender porque terei prova presencial e sem aprender nada farei. precisava agradecer a todos aqui e dizer que tenho mais tres dias apenas para estudar.
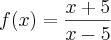
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por MarceloFantini » Qua Nov 14, 2012 19:24
por MarceloFantini » Qua Nov 14, 2012 19:24
Silmara, para derivar esta função perceber que temos um
quociente de funções, ou seja, uma razão (divisão) de duas funções. Para colocar em termos explícitos, as funções são

e
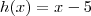
. Então temos que
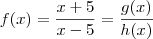
.
Pelas regras de derivação, sabemos que a derivada do quociente é

.
Aplicando na função em questão, segue que


.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por SILMARAKNETSCH » Qua Nov 14, 2012 21:52
por SILMARAKNETSCH » Qua Nov 14, 2012 21:52
agradeço o etapa a etapa agora vou treinar mudando numeros assim sei que praticando um pouco ajuda a aprender dai parto para entender de vez a formula e conceitos que estes jamais deixarão de me ajudar a fazer outros exercícios. abraço. silmara.
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por SILMARAKNETSCH » Qua Nov 14, 2012 21:57
por SILMARAKNETSCH » Qua Nov 14, 2012 21:57
Marcelo seus alunos gostarão muito de aprender com você esse etapa etapa parece num olhar um monstrinho mas seguindo brincando e entendendo com numeros diferentes vamos entendendo de onde e como achar cada coisa e concluir.
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivar uma função
por rcs01 » Qui Abr 30, 2015 09:48
- 0 Respostas
- 2197 Exibições
- Última mensagem por rcs01

Qui Abr 30, 2015 09:48
Cálculo: Limites, Derivadas e Integrais
-
- Derivar utilizando a de função ?
por Charlys Couto » Sex Abr 29, 2011 12:19
- 5 Respostas
- 3332 Exibições
- Última mensagem por Yokotoyota

Qui Fev 04, 2016 04:46
Cálculo: Limites, Derivadas e Integrais
-
- derivar função com módulo
por amanda costa » Sex Jun 01, 2012 01:10
- 4 Respostas
- 4077 Exibições
- Última mensagem por joaofonseca

Sex Jun 01, 2012 18:49
Cálculo: Limites, Derivadas e Integrais
-
- Como derivar esta função: (x^3 + 7x^2 -8).(2x^-3 + x^-4)
 por fabio carvalho » Dom Mai 29, 2016 01:50
por fabio carvalho » Dom Mai 29, 2016 01:50
- 1 Respostas
- 2611 Exibições
- Última mensagem por nakagumahissao

Dom Mai 29, 2016 21:43
Cálculo: Limites, Derivadas e Integrais
-
- quais os Passos para derivar essa função
por Netolucena » Seg Nov 05, 2012 20:43
- 2 Respostas
- 8337 Exibições
- Última mensagem por e8group

Seg Nov 05, 2012 21:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
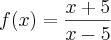


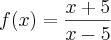

 e
e 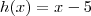 . Então temos que
. Então temos que 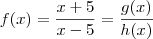 .
. .
.
 .
.








