não estou conseguindo se algum dos colegas do forum conseguir ...
A)sendo F(X)=(3x-4)/6 F:IR é IR,então calcule f -¹(X)
B) sejam as funções reais F(X)=4X-15 e G(X)=x²+2x-3 determine FOG e GOF
C) e resolver a inequação: -x²-7x+10>0
vlw



 , a inversa (talvez) satisfaz ,
, a inversa (talvez) satisfaz ,  .
.  e
e  são subconjuntos . Neste caso especifico do seu exercício ,
são subconjuntos . Neste caso especifico do seu exercício ,  e
e  .
.  , você precisar trocar " y" com " " x " e isolar "y" . Grosseiramente , o que era o dominio " x " virou a imagem "y" , isto é a inversa de uma função . A notação
, você precisar trocar " y" com " " x " e isolar "y" . Grosseiramente , o que era o dominio " x " virou a imagem "y" , isto é a inversa de uma função . A notação  denota isso .
denota isso . 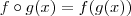 e
e 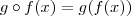 .
. 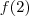 e
e 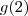 , você obterá as composições de funções trocando " x " por
, você obterá as composições de funções trocando " x " por  , se você quer
, se você quer  o outro caso é semelhante a este .
o outro caso é semelhante a este . 

 .Então ,
.Então , 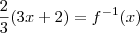 , Pois ,
, Pois , 
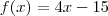 . Logo ,
. Logo , 
 ? Basta lembra que de acordo com o enunciado ,
? Basta lembra que de acordo com o enunciado ,  .
.  deixo para vc tentar .
deixo para vc tentar . 
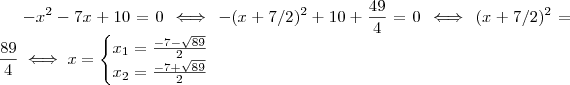

 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: