[Função Modular] Outras perspectivas

[Jhenrique]

Saudações!

Estive percebendo que certas calculadoras eletrônicas, inclusive o GeoGebra, chamam o módulo de x como uma função, abs(x)... então, por acaso cheguei a pensar: "e se de fato o módulo for uma função, será que é ou será que é apenas uma operação?"

Imaginei que se o módulo de fato fosse uma função, então ele teria uma inversa, x = abs?¹(y), que deveria ser igual a x = rel(y) e se existe uma função relativa, existe uma relativa inversa, que é igual a absoluta, rel?¹(x) = y, ou seja, abs(x) = y.

Em matemática pura, isso existe, está certo, faz sentido?

vlw,

[MarceloFantini]

Imaginei que se o módulo de fato fosse uma função, então ele teria uma inversa,[...]

Errado. Nem toda função tem inversa, apenas as que são bijetoras. Para que seja função, basta que cada ponto do domínio tenha uma única imagem no contradomínio (as imagens de dois elementos podem coincidir, mas um dado elemento NUNCA pode ter duas imagens!).

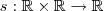Além disso, toda operação é uma função. A operação de soma entre dois números reais, por exemplo, é uma função que recebe dois números reais e retorna outro por meio da soma, ou seja, .