(FUVEST) Calcule a área de um triângulo equilátero com um vértice no ponto (0,0) e os outros sobre a parábola
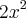
Resposta:
![\frac{3\sqrt[2]{5}}{4} \frac{3\sqrt[2]{5}}{4}](/latexrender/pictures/8f9f6e69690a542ce7f8ca35a8f4a1d8.png)

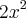
![\frac{3\sqrt[2]{5}}{4} \frac{3\sqrt[2]{5}}{4}](/latexrender/pictures/8f9f6e69690a542ce7f8ca35a8f4a1d8.png)

 . Sejam
. Sejam 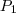 e
e 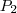 os pontos. Teremos que suas coordenadas são
os pontos. Teremos que suas coordenadas são 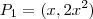 e
e  .
. 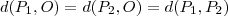 . Daí,
. Daí, 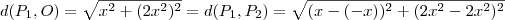 .
.  , que será o lado do triângulo, e usar
, que será o lado do triângulo, e usar 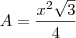 .
.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante