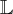 o operador Transformada de Laplace, isto é,
o operador Transformada de Laplace, isto é, 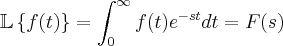 .
.Gostaria de obter uma identidade para a seguinte Transformada:
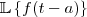 . Isto é, qual a relação da transformada da
. Isto é, qual a relação da transformada da  para com a mesma função mas linearmente deslocada?
para com a mesma função mas linearmente deslocada?Eu conheço a propriedade
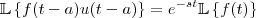 , onde
, onde 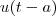 é a Função de Heaviside.
é a Função de Heaviside.Mas e se a função
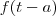 não estiver multiplicada por
não estiver multiplicada por 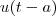 ?
?


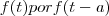 .
.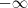 a
a 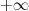
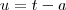
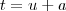 , onde vc vai substituir no expoente do termo
, onde vc vai substituir no expoente do termo 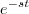 :
: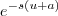
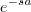 da integral.
da integral.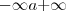 .
. 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)