Seja
 em que a, b e c são números reais. A imagem de f é a semirreta ]?1,
em que a, b e c são números reais. A imagem de f é a semirreta ]?1, ?[ e o gráfico de f intercepta os eixos coordenados nos pontos (1, 0) e (0, ?3/4). Então,
o produto abc vale?

 em que a, b e c são números reais. A imagem de f é a semirreta ]?1,
em que a, b e c são números reais. A imagem de f é a semirreta ]?1, 
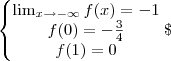







 [, há a coordenada (0,0) ?
[, há a coordenada (0,0) ?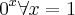


 aumentar ou diminuir.
aumentar ou diminuir.
Mariana Martin escreveu:Agora entendi a minha dúvida, só que não compreendi seu questionamento sobre o deslocamento para a esquerda ou direita se o "c" da funçãoaumentar ou diminuir.
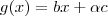 , onde
, onde  é um escalar . Fazendo uma analogia se g e f fosse uma reta r e s por exemplo teríamos duas retas paralelas . Pense assim ...
é um escalar . Fazendo uma analogia se g e f fosse uma reta r e s por exemplo teríamos duas retas paralelas . Pense assim ...
santhiago escreveu:Agora entendi a minha dúvida, só que não compreendi seu questionamento sobre o deslocamento para a esquerda ou direita se o "c" da função f(x) = bx+c aumentar ou diminuir.
Mariana Martin escreveu:Note que " c " é o termo que intercepta o eixo y . Basta tomar f(0) e observa o mesmo . Assim f desloca (com a mesma direção) em relação ao eixo y a medida que c varia .
OBS.: Citei direção porque a inclinação da reta é independente do termo c .
Para você visualizar , imagine uma outra função , por exemplo : , onde é um escalar . Fazendo uma analogia se g e f fosse uma reta r e s por exemplo teríamos duas retas paralelas . Pense assim ...

 --------------------- i)
--------------------- i)  ---------------------ii)
---------------------ii)  se e somente se
se e somente se  (porque ? Resposta: deixo a você refletir e chegar a conclusão ,ok. ) e
(porque ? Resposta: deixo a você refletir e chegar a conclusão ,ok. ) e 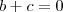 , ou seja :
, ou seja : .
.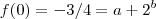
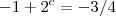
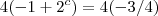




 , portanto
, portanto 


Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.