Esse é um problema simples de vazão.
A vazão da torneira 1 é dada por
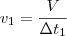
,
e da torneira dois por
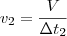
,
onde

é o volume total do reservatório e os deltas de tempo são 3 h e 15 h, respectivamente.
Agora, como as duas torneiras funcionam juntas a vazão resultante será a soma das vazões de cada um individualmente. Ou seja
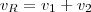
.
Tomando ainda que a vazão resultante encherá a fração
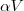
do tanque em um tempo
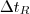
, então
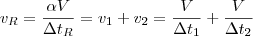
.
Portanto,
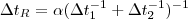
.
Veja que se a vazão resultante deve encher todo o tanque então temos de considerar

, que sugere a solução clássica deste problema. (:
Substituindo os valores você deve calcular 1h40min.


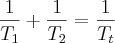
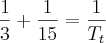
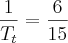
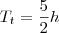
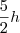 .
. --------------------------------- k
--------------------------------- k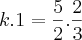
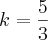

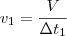 ,
,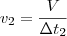 ,
, é o volume total do reservatório e os deltas de tempo são 3 h e 15 h, respectivamente.
é o volume total do reservatório e os deltas de tempo são 3 h e 15 h, respectivamente.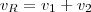 .
.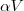 do tanque em um tempo
do tanque em um tempo 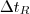 , então
, então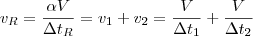 .
.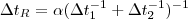 .
. , que sugere a solução clássica deste problema. (:
, que sugere a solução clássica deste problema. (:
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.