dada a função quadratica definida por f(x)=
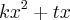 e os pontos A(-2,0) e B (u,0) com u sendo diferenre de -2 pertecentes ao grafico de F, determine o valor de u.
e os pontos A(-2,0) e B (u,0) com u sendo diferenre de -2 pertecentes ao grafico de F, determine o valor de u.
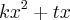 e os pontos A(-2,0) e B (u,0) com u sendo diferenre de -2 pertecentes ao grafico de F, determine o valor de u.
e os pontos A(-2,0) e B (u,0) com u sendo diferenre de -2 pertecentes ao grafico de F, determine o valor de u.

 .
. , a mim leva-me a pensar que u=0. Apesar de que com a insuficiente informação que é dada, não se pode afirmar com certeza qual o valor de u.
, a mim leva-me a pensar que u=0. Apesar de que com a insuficiente informação que é dada, não se pode afirmar com certeza qual o valor de u.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

