bom dia
eu tenho uma duvida, é a seguinte:
Dê um exemplo de uma função racional em que o zero do denominador ( chamemos a) não seja uma assimptota vertical da funcao
o modo de calcular assimptota é com o limite da função, neste caso se por exemplo 1 fosse zero do denominador , teria que se calcular o limite da função quando x tende para 1 por valores negativos e positivos, se o limite der um infinito entao x=1 é assimptota da funçao
eu quero um caso em que isto não acontece
eu já tentei fazer mas o problema é que sempre que eu escrevo uma função racional o zero do denominador é assimptota vertical
por favor expliquem o raciocinio




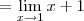

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)