 por Ana_Rodrigues » Ter Jan 24, 2012 17:46
por Ana_Rodrigues » Ter Jan 24, 2012 17:46
Eu não entendo essas transformações!
Por exemplo:
1)
![cos(sen{}^{-1})=\sqrt[]{1-{x}^{2}} cos(sen{}^{-1})=\sqrt[]{1-{x}^{2}}](/latexrender/pictures/b50d12b10123863eeb4b7ab152fc4d65.png)
ou então:
2)
![sen(tg{}^{-1}x)=\frac{x}{\sqrt[]{1+{x}^{2}}} sen(tg{}^{-1}x)=\frac{x}{\sqrt[]{1+{x}^{2}}}](/latexrender/pictures/f44a1203191ba2b62e324ad4720e6ee6.png)
Não entendo essas simplificações. Não sei como chegar aos resultados mostrados.
Peço a quem souber, que me ajude a entender!
-
Ana_Rodrigues
- Usuário Parceiro

-
- Mensagens: 51
- Registrado em: Seg Nov 14, 2011 09:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Ter Jan 24, 2012 19:47
por LuizAquino » Ter Jan 24, 2012 19:47
Ana_Rodrigues escreveu:1)
![\cos(\textrm{sen}^{-1}\, x)=\sqrt[]{1-{x}^{2}} \cos(\textrm{sen}^{-1}\, x)=\sqrt[]{1-{x}^{2}}](/latexrender/pictures/f02af85cefa241ba4977c7f25b5ee88f.png)
Você deve saber que:
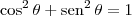
Disso podemos concluir que:
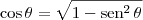
(se

for um ângulo do primeiro ou do quarto quadrante).
Considere agora o ângulo

. Suponha que ele seja do primeiro ou do quarto quadrante. Temos que:
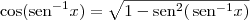
Você deve saber que

representa a função inversa do seno.
Além disso, você deve saber que se

é a função inversa de
f, então é válida a propriedade
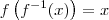
.
Por outro lado, você também deve saber que

.
Usando essas informações, temos que:
![\cos (\textrm{sen}^{-1} x) = \sqrt{1 - \left[\textrm{sen} (\,\textrm{sen}^{-1} x)\right]^2} = \sqrt{1-x^2} \cos (\textrm{sen}^{-1} x) = \sqrt{1 - \left[\textrm{sen} (\,\textrm{sen}^{-1} x)\right]^2} = \sqrt{1-x^2}](/latexrender/pictures/ed9fac86e2c1b54be281083c16654d9c.png)
Ana_Rodrigues escreveu:2)
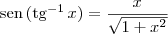
A ideia é parecida com a anterior.
Mas lembre-se que usando
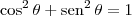
e

podemos obter que:
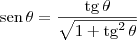
(se

for um ângulo do primeiro ou do terceiro quadrante).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Ana_Rodrigues » Ter Jan 24, 2012 22:33
por Ana_Rodrigues » Ter Jan 24, 2012 22:33
Muito obrigada!

-
Ana_Rodrigues
- Usuário Parceiro

-
- Mensagens: 51
- Registrado em: Seg Nov 14, 2011 09:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- funções inversas
por Edgard Guarido » Sex Mar 07, 2014 18:53
- 2 Respostas
- 2599 Exibições
- Última mensagem por Edgard Guarido

Qui Mar 13, 2014 15:54
Funções
-
- Funções circulares inversas
por Ananda » Qui Mar 20, 2008 20:03
- 2 Respostas
- 4800 Exibições
- Última mensagem por Ananda

Seg Mar 24, 2008 17:13
Trigonometria
-
- funçoes circulares inversas
por Thassya » Sex Mai 29, 2009 11:29
- 3 Respostas
- 2515 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 10:18
Trigonometria
-
- Funções Tirgonométricas Inversas
por geriane » Seg Jul 05, 2010 12:06
- 1 Respostas
- 1203 Exibições
- Última mensagem por Tom

Seg Jul 05, 2010 13:07
Trigonometria
-
- trigonometria-funçoes inversas
por henrique_mat » Seg Ago 23, 2010 18:57
- 4 Respostas
- 2597 Exibições
- Última mensagem por henrique_mat

Ter Ago 24, 2010 20:59
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![cos(sen{}^{-1})=\sqrt[]{1-{x}^{2}} cos(sen{}^{-1})=\sqrt[]{1-{x}^{2}}](/latexrender/pictures/b50d12b10123863eeb4b7ab152fc4d65.png)
![sen(tg{}^{-1}x)=\frac{x}{\sqrt[]{1+{x}^{2}}} sen(tg{}^{-1}x)=\frac{x}{\sqrt[]{1+{x}^{2}}}](/latexrender/pictures/f44a1203191ba2b62e324ad4720e6ee6.png)

![cos(sen{}^{-1})=\sqrt[]{1-{x}^{2}} cos(sen{}^{-1})=\sqrt[]{1-{x}^{2}}](/latexrender/pictures/b50d12b10123863eeb4b7ab152fc4d65.png)
![sen(tg{}^{-1}x)=\frac{x}{\sqrt[]{1+{x}^{2}}} sen(tg{}^{-1}x)=\frac{x}{\sqrt[]{1+{x}^{2}}}](/latexrender/pictures/f44a1203191ba2b62e324ad4720e6ee6.png)

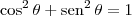
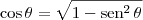 (se
(se  for um ângulo do primeiro ou do quarto quadrante).
for um ângulo do primeiro ou do quarto quadrante). . Suponha que ele seja do primeiro ou do quarto quadrante. Temos que:
. Suponha que ele seja do primeiro ou do quarto quadrante. Temos que: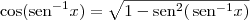
 representa a função inversa do seno.
representa a função inversa do seno. é a função inversa de f, então é válida a propriedade
é a função inversa de f, então é válida a propriedade 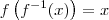 .
. .
.![\cos (\textrm{sen}^{-1} x) = \sqrt{1 - \left[\textrm{sen} (\,\textrm{sen}^{-1} x)\right]^2} = \sqrt{1-x^2} \cos (\textrm{sen}^{-1} x) = \sqrt{1 - \left[\textrm{sen} (\,\textrm{sen}^{-1} x)\right]^2} = \sqrt{1-x^2}](/latexrender/pictures/ed9fac86e2c1b54be281083c16654d9c.png)
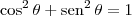 e
e  podemos obter que:
podemos obter que: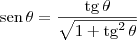 (se
(se  for um ângulo do primeiro ou do terceiro quadrante).
for um ângulo do primeiro ou do terceiro quadrante).

