 por QuimG » Sáb Nov 19, 2011 22:53
por QuimG » Sáb Nov 19, 2011 22:53
Boa noite
Alguem me pode ajudar a resolver aqui 5 questões referentes a uma função?
[/tex]
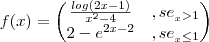
Determine o domínio da função
A aderência e o interior do Df
Estude a função f quanto à continuidade.
Justificar se f é diferenciável para x=1.
Calcular, usando a definição de derivada num ponto, f' (1-).
Muito obrigados.
Cumprimentos
-
QuimG
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Nov 19, 2011 22:34
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informática
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [descobrir valor para domínio] Domínio da função
por Zebra-LNX » Sáb Jun 16, 2012 12:26
- 1 Respostas
- 3262 Exibições
- Última mensagem por MarceloFantini

Ter Jun 19, 2012 22:18
Funções
-
- [Domínio] Determinar domínio a partir da função
por +danile10 » Qui Fev 07, 2013 21:33
- 1 Respostas
- 2891 Exibições
- Última mensagem por e8group

Qui Fev 07, 2013 22:38
Funções
-
- Tenho dificuldades, preciso de ajudo urgente!!!
por Emanuel » Sáb Abr 03, 2010 10:12
- 3 Respostas
- 2628 Exibições
- Última mensagem por Emanuel

Sáb Abr 03, 2010 13:03
Geometria Analítica
-
- [Domínio da Função] A função abaixo é definida f(x)=x²-3x
por Tiago Neto » Qui Mai 30, 2013 20:58
- 0 Respostas
- 1776 Exibições
- Última mensagem por Tiago Neto

Qui Mai 30, 2013 20:58
Funções
-
- dominio da funçao
por Thassya » Sex Mai 29, 2009 11:26
- 4 Respostas
- 5182 Exibições
- Última mensagem por Marcampucio

Dom Mai 31, 2009 18:58
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
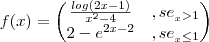


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.