por Sabrina » Sáb Mai 09, 2009 19:16
por Molina » Dom Mai 10, 2009 14:18
e uma linha vertical e chamamos de 
). Só que agora como a variável é 
, a linha horizontal terá que ser chamada de e a reta vertical vamos chamar, por exemplo de 
. Próximo passo é dar valores pra e descobrir que valor assume em . Faça isso com o maior quantidade de ponto possíveis. Sempre dando valor pra e descobrindo .
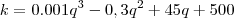
, é igual a 500.
por Douglas13 » Qua Dez 02, 2015 09:40
por concurseironf » Qui Ago 21, 2014 12:24
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será , mas negativo pois tem de ser no quarto quadrante. Se 
, então 
. Como módulo é um: 
.
.