 por maria cleide » Seg Out 24, 2011 20:00
por maria cleide » Seg Out 24, 2011 20:00
Determine o(s) valor(es) de K para que o valor mínimo da função quadrática
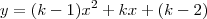
seja

e assinale a opção correta.
A-( )
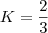
B-( )

ou

C-( )

D-( )
 Como resolvi :
Como resolvi : Encontrei o Yv usando a fórmula
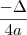
, achando como resposta

alternativa B.
Mas o gabarito constou como certa a alternativa de letra D, ou seja, o Xv. Portanto tenho dúvida se "o valor mínimo da função" é o XV ou o Yv.
Por favor me ajudem pois amanhã é o pedido de revisão do gabarito.
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Valor mínimo
 por FilipeCaceres » Qui Mai 26, 2011 19:53
por FilipeCaceres » Qui Mai 26, 2011 19:53
- 13 Respostas
- 8425 Exibições
- Última mensagem por demolot

Sex Mai 27, 2011 19:31
Funções
-
- valor mínimo de x real
por studieren » Sáb Mai 01, 2010 17:39
- 6 Respostas
- 2548 Exibições
- Última mensagem por studieren

Qua Mai 05, 2010 04:05
Trigonometria
-
- [Derivadas] Mínimo de função
por vinisoares9 » Dom Jun 24, 2012 00:22
- 2 Respostas
- 1763 Exibições
- Última mensagem por vinisoares9

Dom Jun 24, 2012 02:58
Cálculo: Limites, Derivadas e Integrais
-
- Função quadrática - máximo e mínimo
por PatriciaFerreira » Qui Abr 23, 2015 18:58
- 0 Respostas
- 1542 Exibições
- Última mensagem por PatriciaFerreira

Qui Abr 23, 2015 18:58
Funções
-
- Ponto Máximo e Mínimo de uma função.
por lucasowner » Qui Ago 13, 2015 03:05
- 1 Respostas
- 2008 Exibições
- Última mensagem por nakagumahissao

Qui Ago 13, 2015 15:29
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
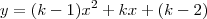 seja
seja  e assinale a opção correta.
e assinale a opção correta.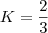
 ou
ou 


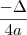 , achando como resposta
, achando como resposta  alternativa B.
alternativa B.
