Uma maquina copiadora apos a compra tem seu valor depreciado a uma taxa de 11,5% ao ano.Sabendo que o valor pode ser expresso por uma função exponencial e que o valor na compra é de 68.500.
1-Obtenha o valor V como função dos anos apos a compra da maquina copiadora ,isto é V=f(x).
2-Obtenha o valor da maquina copiadora apos 1,5,e 10 anos da compra.
3-Esboce o grafico de V(X).
4-Apos quanto tempo o valor da maquina será a metade do valor inicial?



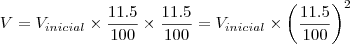
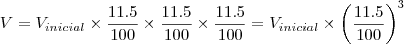
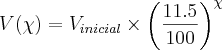


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)