 por 380625 » Qui Set 15, 2011 03:51
por 380625 » Qui Set 15, 2011 03:51
Tenho a seguinte proposição:
Seja f uma função periodica de período p então:
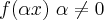
é periodica de período p\

.
Quando vou provar o que faço:
1 - Defino h(x) =

e assim temos que
Dh = { x

|

Df }
Não consigo entender o porque

Df.
-
380625
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sex Fev 18, 2011 17:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Qui Set 15, 2011 11:01
por LuizAquino » Qui Set 15, 2011 11:01
380625 escreveu:1 - Defino h(x) =

e assim temos que
Dh = { x

|

Df }
Não consigo entender o porque
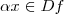
.
É necessário que

esteja no domínio de
f, caso contrário não seria possível calcular
h(x).
Vejamos um exemplo. Considere a função

. Como você deve saber,
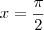
não faz parte o domínio de
f (se você não se recorda disso, então faça uma pequena revisão sobre a função tangente).
Considere que você tenha definido a função
h(x) =
f(3x). Note que para
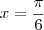 não podemos calcular
não podemos calcular o valor de
h, pois temos

, entretanto como vimos antes a função
f não está definida para esse valor.
Conclusão: o valor
x está no domínio de
h apenas se o valor 3
x estiver no domínio de
f.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3423 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
-
- [Funções] Domínio e a imagem de funções
 por concurseironf » Qui Ago 21, 2014 12:24
por concurseironf » Qui Ago 21, 2014 12:24
- 1 Respostas
- 4191 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 22, 2014 20:11
Funções
-
- [Funções] questões de funções
por Zandrojr » Qua Ago 31, 2011 11:39
- 0 Respostas
- 3137 Exibições
- Última mensagem por Zandrojr

Qua Ago 31, 2011 11:39
Funções
-
- Funções
por Revelants » Dom Out 05, 2008 15:07
- 1 Respostas
- 3387 Exibições
- Última mensagem por Molina

Dom Out 05, 2008 15:53
Cálculo: Limites, Derivadas e Integrais
-
- Funçoes
por Luna » Seg Set 28, 2009 20:02
- 1 Respostas
- 2994 Exibições
- Última mensagem por Marcampucio

Seg Set 28, 2009 21:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
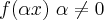 é periodica de período p\
é periodica de período p\ .
. e assim temos que
e assim temos que |
| Df }
Df } Df.
Df.
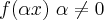 é periodica de período p\
é periodica de período p\ .
. e assim temos que
e assim temos que |
| Df }
Df } Df.
Df.
e assim temos que
|
Df }
.
 esteja no domínio de f, caso contrário não seria possível calcular h(x).
esteja no domínio de f, caso contrário não seria possível calcular h(x). . Como você deve saber,
. Como você deve saber, 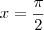 não faz parte o domínio de f (se você não se recorda disso, então faça uma pequena revisão sobre a função tangente).
não faz parte o domínio de f (se você não se recorda disso, então faça uma pequena revisão sobre a função tangente).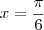 não podemos calcular o valor de h, pois temos
não podemos calcular o valor de h, pois temos  , entretanto como vimos antes a função f não está definida para esse valor.
, entretanto como vimos antes a função f não está definida para esse valor.