Olá Zekinha! O que você tem que entender é o seguinte: uma função linear é uma
reta, e portanto pra descrevê-la temos que saber pelo menos 2 pontos. Como conseguir esses dois pontos? Se você já tem a função, basta escolher quaisquer dois pontos! Note que a função relaciona um ponto y, que está na vertical (eixo das ordenadas) com um ponto x, que está na horizontal (eixo das abscissas).
Escolhendo um valor para x, você obtém um correspondente em y, e assim consegue um ponto. Escolhendo um outro valor para x, ou mesmo um outro valor para y, você obtém o correspondente no outro eixo (ou seja, escolhendo um x você obtém um y, e escolhendo um y você obtém um x), conseguindo assim o outro ponto. Agora, basta colocá-los no gráficos e ligar usando a régua, formando uma reta.
Respondendo a sua pergunta, você pode pegar qualquer ponto! Pode ser

,

,
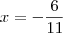
,
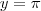
,
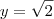
, tanto faz, o importante é que você obtenha dois pontos que satisfaçam a relação dada. Por último, existem infinitas funções, dos mais variados tipos, formas, inclusive funções que ninguém sabe colocar uma regra mas que sabemos que satisfaz propriedades que nos interessam.
Espero ter ajudado agora. Um abraço.

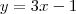

 porque que é para
porque que é para 

 e
e  . não entendo
. não entendo

 .
.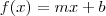 .Em que
.Em que  a zero (y=0) queremos calcular a abcissa do ponto em que o gráfico interceta o eixo Ox.
a zero (y=0) queremos calcular a abcissa do ponto em que o gráfico interceta o eixo Ox.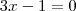
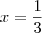


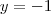


 neh? correto?
neh? correto? ? isso?
? isso? ?
?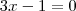 sempre no meu gabarito, fala assim:
sempre no meu gabarito, fala assim: ?
?  ?
? 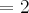 ... ?
... ? ,
,  ,
, 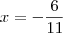 ,
, 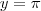 ,
, 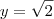 , tanto faz, o importante é que você obtenha dois pontos que satisfaçam a relação dada. Por último, existem infinitas funções, dos mais variados tipos, formas, inclusive funções que ninguém sabe colocar uma regra mas que sabemos que satisfaz propriedades que nos interessam.
, tanto faz, o importante é que você obtenha dois pontos que satisfaçam a relação dada. Por último, existem infinitas funções, dos mais variados tipos, formas, inclusive funções que ninguém sabe colocar uma regra mas que sabemos que satisfaz propriedades que nos interessam.

