 por Abner » Sex Jun 24, 2011 22:13
por Abner » Sex Jun 24, 2011 22:13
Considere a seguinte fórmula para x?? : f (x)=x?1
x?2 .
a) Qual é o Dom( f ) , ou seja, o domínio de f(x), e qual é a Im(f ) , ou seja
a imagem de f(x)?
b) Mostre que a função f é inversível no seu domínio e calcule a função
inversa. Qual é o domínio da função inversa?
a)Seria o dominio N ou seja todos os numeros naturais? e a imagem Z maiores ou igqual a -1?
b)x=y-1 essa seria sua inversa?Se puderem me esclarecer....
-
Abner
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Qua Jan 26, 2011 18:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Abner » Sex Jun 24, 2011 22:21
por Abner » Sex Jun 24, 2011 22:21
desculpe errei é f (x)=x?1/
x?2 .
-
Abner
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Qua Jan 26, 2011 18:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Sáb Jun 25, 2011 01:00
por MarceloFantini » Sáb Jun 25, 2011 01:00
Abner, confirme:
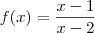
ou
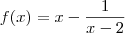
? Por favor, procure usar latex nas suas próximas postagens.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Abner » Sáb Jun 25, 2011 16:21
por Abner » Sáb Jun 25, 2011 16:21
Marcelo e a primeira f(x)=x-1/x-2.Quanto ao latex entrei mas não consegui achar a barra de divisão....desculpe
-
Abner
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Qua Jan 26, 2011 18:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por arima » Sáb Jun 25, 2011 18:41
por arima » Sáb Jun 25, 2011 18:41
NNeste exercicio só estou com duvida para mostrar que ela é inversivel no dóminio.
D(f)={xpertence aos reais /xdiferente de 2} e imagem temos y pertence aos reais tal que y diferente de um} use simbolos pois nao achei aqui para usar.
-
arima
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sáb Out 23, 2010 18:25
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por arima » Sáb Jun 25, 2011 18:43
por arima » Sáb Jun 25, 2011 18:43
e o dominio da funçao inversa é a imagem da funçao sem ser inversa.
-
arima
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sáb Out 23, 2010 18:25
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por Abner » Sáb Jun 25, 2011 18:57
por Abner » Sáb Jun 25, 2011 18:57
valeu Arima.E quanto ao exer 1(Sendo O a origem de um sistema de coordenadas, e dado o ponto A = (6, 8),
encontre as coordenadas do ponto B tal que o segmento OB tem comprimento 4 ) vc conseguiu resolver?
-
Abner
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Qua Jan 26, 2011 18:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por arima » Ter Jun 28, 2011 13:43
por arima » Ter Jun 28, 2011 13:43
Ainda não sei como mostrar que ela é inversivel no seu dominio.
Alguem pode me ajudar?
-
arima
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sáb Out 23, 2010 18:25
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por joaofonseca » Qua Jun 29, 2011 19:01
por joaofonseca » Qua Jun 29, 2011 19:01
É sabido que para uma função ter inversa, ou tido de outra forma, para que a inversa de uma função seja também uma função é necessário observar:

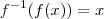
Pegando na função
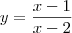
substituindo y por x reciprocamente e resolvendo em ordem a y, obtem-se:
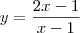
Pode-se já concluir que o contradominio da função
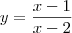
são todos os números reais exeto o 1.
Para saber se a função é invertível basta fazer as devidas substituições nas duas expressões iniciais e verificar se o resultado é x em ambas.
No que respeita ao Dominio e Contradominio aqui fica o gráfico para provar:

- Ecra#2.jpg (10.42 KiB) Exibido 3893 vezes
A assintota vertical é o valor excluído do dominio. A assintota horizontal é o valor excluíído do contradominio.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3428 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
-
- [Funções] Domínio e a imagem de funções
 por concurseironf » Qui Ago 21, 2014 12:24
por concurseironf » Qui Ago 21, 2014 12:24
- 1 Respostas
- 4195 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 22, 2014 20:11
Funções
-
- [Funções] questões de funções
por Zandrojr » Qua Ago 31, 2011 11:39
- 0 Respostas
- 3140 Exibições
- Última mensagem por Zandrojr

Qua Ago 31, 2011 11:39
Funções
-
- Funções
por Revelants » Dom Out 05, 2008 15:07
- 1 Respostas
- 3390 Exibições
- Última mensagem por Molina

Dom Out 05, 2008 15:53
Cálculo: Limites, Derivadas e Integrais
-
- Funçoes
por Luna » Seg Set 28, 2009 20:02
- 1 Respostas
- 2996 Exibições
- Última mensagem por Marcampucio

Seg Set 28, 2009 21:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


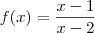 ou
ou 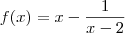 ? Por favor, procure usar latex nas suas próximas postagens.
? Por favor, procure usar latex nas suas próximas postagens.


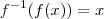
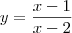 substituindo y por x reciprocamente e resolvendo em ordem a y, obtem-se:
substituindo y por x reciprocamente e resolvendo em ordem a y, obtem-se: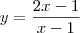



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.