 por jamiel » Qua Jun 22, 2011 15:49
por jamiel » Qua Jun 22, 2011 15:49
Sabendo que

,

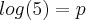
, calcule os logaritmos abaixo, em função de m, n e p:
a)

b)
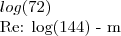
c)
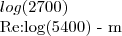
d)
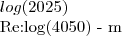
e)
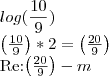
f)
![log(\sqrt[4]{\frac{1944}{125}})
Re:\left(log(\sqrt[4]{\frac{1944}{125}})*2 \right)=\left(log(\frac{\frac{1944}{125}}{2} \right)
\left(log(\frac{\frac{1944}{125}}{2}) - m\right) log(\sqrt[4]{\frac{1944}{125}})
Re:\left(log(\sqrt[4]{\frac{1944}{125}})*2 \right)=\left(log(\frac{\frac{1944}{125}}{2} \right)
\left(log(\frac{\frac{1944}{125}}{2}) - m\right)](/latexrender/pictures/4a2d57e167beebbf348978b392e67849.png)
Eu resolvi do meu jeito, mas não estou conseguindo entender a resolução do livro. Alguém pode me ajudar?
Gabarito do livro:
a) m+n+p
b) 3m+2n
c) 2m+3n+2p
d) 4n+2p
e) m+p-2n
f) (3m+5n-3p)/4
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por LuizAquino » Qua Jun 22, 2011 16:00
por LuizAquino » Qua Jun 22, 2011 16:00
Primeiro, você tem que escrever o logaritmando como o resultado de operações de produto ou divisão entre 2, 3 ou 5. Em seguida, basta utilizar as propriedades dos logaritmos.
Por exemplo:
a)
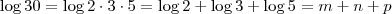
.
(...)
e)
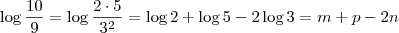
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jamiel » Qua Jun 22, 2011 17:17
por jamiel » Qua Jun 22, 2011 17:17
rsrsrsr
A maneira q eu resolvi foi muito louca, mas deu o resultado também.
Entendi o q vc quis dizer, fui tirando m.m.c e encontrando quantas vezes a letras se encaixariam. Putz! Valeu mesmo, cara. Vou tentar fazer aquela q tem raiz agora!
flw ...
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função Exponencial - Tenso!
por jamiel » Sáb Jun 18, 2011 03:12
- 4 Respostas
- 2542 Exibições
- Última mensagem por jamiel

Dom Jun 19, 2011 17:54
Funções
-
- Função Log - tenso dúvida
por jamiel » Dom Jun 26, 2011 16:40
- 10 Respostas
- 7405 Exibições
- Última mensagem por MarceloFantini

Seg Jun 27, 2011 00:18
Funções
-
- Limite tenso
por Isabela Sa » Qua Jun 29, 2011 19:27
- 1 Respostas
- 1265 Exibições
- Última mensagem por Claudin

Qua Jun 29, 2011 19:51
Cálculo: Limites, Derivadas e Integrais
-
- Sisteminha tenso!!
por bigolasMan » Sex Mai 04, 2012 00:21
- 1 Respostas
- 1132 Exibições
- Última mensagem por Russman

Sex Mai 04, 2012 00:37
Sistemas de Equações
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5562 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ,
, 
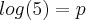 , calcule os logaritmos abaixo, em função de m, n e p:
, calcule os logaritmos abaixo, em função de m, n e p:
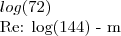
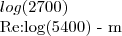
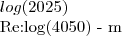
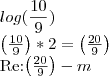
![log(\sqrt[4]{\frac{1944}{125}})
Re:\left(log(\sqrt[4]{\frac{1944}{125}})*2 \right)=\left(log(\frac{\frac{1944}{125}}{2} \right)
\left(log(\frac{\frac{1944}{125}}{2}) - m\right) log(\sqrt[4]{\frac{1944}{125}})
Re:\left(log(\sqrt[4]{\frac{1944}{125}})*2 \right)=\left(log(\frac{\frac{1944}{125}}{2} \right)
\left(log(\frac{\frac{1944}{125}}{2}) - m\right)](/latexrender/pictures/4a2d57e167beebbf348978b392e67849.png)


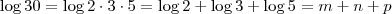 .
.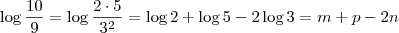 .
.

 .
.



