Boa noite, Fabricio.
Achei mais fácil usar a lógica do que uma função para descrever estes produtos. Essa não é a única resolução, vai de você aceitar ou não. Veja:
P1 é formado por 20% do componente A e 80% do componente B:
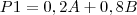
P2 é formado por 10% do componente A e 90% do componente B:
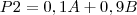
Agora vamos analisar: Para fazer 1 litro de P1 são necessários 0,2 de A e 0,8 de B:


...
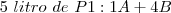
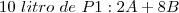
Em paralelo a isso, faça o mesmo para P2: Para fazer 1 litro de P2 são necessários 0,1 de A e 0,9 de B:
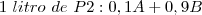
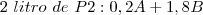
...
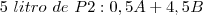
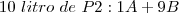
Sabemos que o total de litros de P1 e P2 é 15 litros (2 litros + 13 litros). Ou seja, temos que achar um equilíbrio entre P1 e P2 que somado de 15 litros (ex: 1l P1 + 14l P2; 2l P1 + 13l P2; ...). Mas não só isso. O número na frente do A dos dois produtos tem que ter soma 2 e o número na frente do B dos dois produtos tem que ter soma 13.
A única solução que satisfaz essas três condições são:
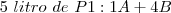
e
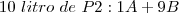



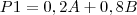
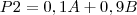


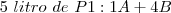
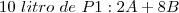
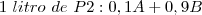
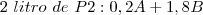
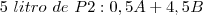
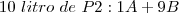



 , avisa que eu resolvo.
, avisa que eu resolvo.

