 por jamiel » Sáb Jun 18, 2011 03:12
por jamiel » Sáb Jun 18, 2011 03:12
Resolva a equação:
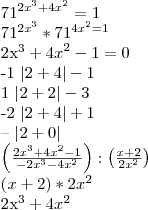
Depois de tudo, eu chego a conclusão de q os valores de "x" são 0, 0 e -2. No entanto, surgiu uma dúvida: Como fica a situação desse "-1" em todo o processo? Eu comecei com um método de redução de uma função de terceiro para segundo grau, com o "-1" incluso, e, em seguida, parti para a divisão de polinômios. Porém, surgi, outra vez, a dúvida em relação ao "-1", mais uma vez ele permanece como um espectador. Alguém tem uma dica?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por jamiel » Dom Jun 19, 2011 16:31
por jamiel » Dom Jun 19, 2011 16:31
Por isso q o "1" ficava sobrando nos meus calculos. Quer dizer q eu poderia transformar o 1 em 71^0 institivamente? Não entendi muito essa parte. E neste caso,
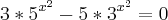
, o q vc faria?
vlw ...
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por LuizAquino » Dom Jun 19, 2011 17:01
por LuizAquino » Dom Jun 19, 2011 17:01
No lado esquerdo da equação nitidamente você tem a base 71 para a potência.
Queremos que no lado direito também apareça uma potência com base 71.
Sendo assim, você deve se fazer a pergunta: 71 elevado a que número tem como resultado o valor 1?
Ora, esse número é 0, pois sabemos que

.
No cado da equação
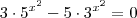
, você precisa aplicar o conhecimento de logaritmos.
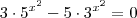




 Sugestão
SugestãoPara estudar os conteúdos de logaritmos (e muito mais), eu recomendo o canal do Nerckie:
http://www.youtube.com/nerckie
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jamiel » Dom Jun 19, 2011 17:54
por jamiel » Dom Jun 19, 2011 17:54
Putz! Valeu, cara.
Eu já tinha visto essas aulas do Nerckie, são muito boas.
O pior é q tentei por logarítmos, mas acho q fiz alguma coisa errada.
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função Log - Tenso
por jamiel » Qua Jun 22, 2011 15:49
- 2 Respostas
- 2063 Exibições
- Última mensagem por jamiel

Qua Jun 22, 2011 17:17
Funções
-
- Função Log - tenso dúvida
por jamiel » Dom Jun 26, 2011 16:40
- 10 Respostas
- 7398 Exibições
- Última mensagem por MarceloFantini

Seg Jun 27, 2011 00:18
Funções
-
- [Função exponencial] Exercício sobre função exponencial
por fff » Ter Jan 07, 2014 17:51
- 3 Respostas
- 4063 Exibições
- Última mensagem por fff

Qua Jan 08, 2014 06:47
Funções
-
- Limite tenso
por Isabela Sa » Qua Jun 29, 2011 19:27
- 1 Respostas
- 1264 Exibições
- Última mensagem por Claudin

Qua Jun 29, 2011 19:51
Cálculo: Limites, Derivadas e Integrais
-
- Sisteminha tenso!!
por bigolasMan » Sex Mai 04, 2012 00:21
- 1 Respostas
- 1131 Exibições
- Última mensagem por Russman

Sex Mai 04, 2012 00:37
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
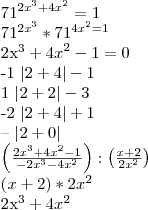




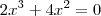


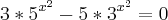 , o q vc faria?
, o q vc faria? .
.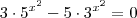 , você precisa aplicar o conhecimento de logaritmos.
, você precisa aplicar o conhecimento de logaritmos.


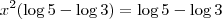


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
