 por andersontricordiano » Qua Mai 11, 2011 14:32
por andersontricordiano » Qua Mai 11, 2011 14:32
Qual é a função real cujo gráfico está representado abaixo:
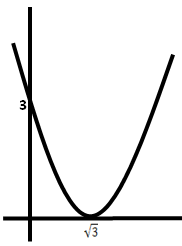
- grafico.gif (3.14 KiB) Exibido 5948 vezes
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Pedro123 » Qua Mai 11, 2011 17:27
por Pedro123 » Qua Mai 11, 2011 17:27
Faça relação de soma e produto, pois você já tem a variável C da equação geral (Ax² +bx + C = f(x)) e você já tem as DUAS raizes, que são iguaiz a raiz de 3, assim faça
Soma = -b/a
produto = c/a, que sai os valores de a,b e c, encontrando a função. Abraços.
Qualquer dúvida pergunte.
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por MarceloFantini » Qua Mai 11, 2011 23:29
por MarceloFantini » Qua Mai 11, 2011 23:29
Considere
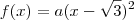
. Temos que

.
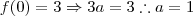
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como é o gráfico desta função, e qual o seu domínio?
por Ronaldobb » Qua Set 19, 2012 15:49
- 1 Respostas
- 1365 Exibições
- Última mensagem por MarceloFantini

Qua Set 19, 2012 22:58
Funções
-
- Qual é o sinal da expressão abaixo?
por andersontricordiano » Sex Ago 12, 2011 22:26
- 3 Respostas
- 4570 Exibições
- Última mensagem por andersontricordiano

Seg Ago 15, 2011 20:29
Trigonometria
-
- Qual o valor de x no calculo abaixo
por andersontricordiano » Qui Mar 22, 2012 02:58
- 4 Respostas
- 6436 Exibições
- Última mensagem por Boyskoy89

Sex Out 28, 2016 05:31
Desafios Difíceis
-
- Qual o radiano formado na figura abaixo
 por andersontricordiano » Seg Jun 06, 2011 15:14
por andersontricordiano » Seg Jun 06, 2011 15:14
- 1 Respostas
- 4137 Exibições
- Última mensagem por DanielFerreira

Seg Jun 06, 2011 18:00
Geometria
-
- Qual a altura do prisma hexagonal descrito abaixo
por andersontricordiano » Qui Nov 24, 2011 16:30
- 1 Respostas
- 4638 Exibições
- Última mensagem por TheoFerraz

Qui Nov 24, 2011 17:32
Geometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




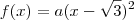 . Temos que
. Temos que  .
. 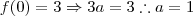 .
.
